สรุปบันทึกการเรียนวิชา statistic 103 สำหรับนักวิทยาศาสตร์ข้อมูล - sprint 05

คำแนะนำจากผู้เขียน - ใครที่สนใจในเรื่องข้อมูล วิชาสถิติถือว่าเป็น foundation ของเรื่องนี้ สำหรับบทความนี้ เป็นสรุปบันทึกการเรียนวิชา statistic 103 สำหรับนักวิทยาศาสตร์ข้อมูล - sprint 05 ขอให้เครดิตแก่ Data Rockie ผู้เปิดโลกทัศน์วิชาด้านข้อมูล โดยที่ผู้เขียนเคยเรียนแล้วไม่เข้าใจแต่ เรียนกับคอร์สนี้แล้วเข้าใจ
Contents
- Review some basic theories?
- Correlation and Linear Regression in Excel
- analysis toolpak
- Correlation and Linear Regression in R
- lm function
- What about logictic?
- Logistic Regression in R
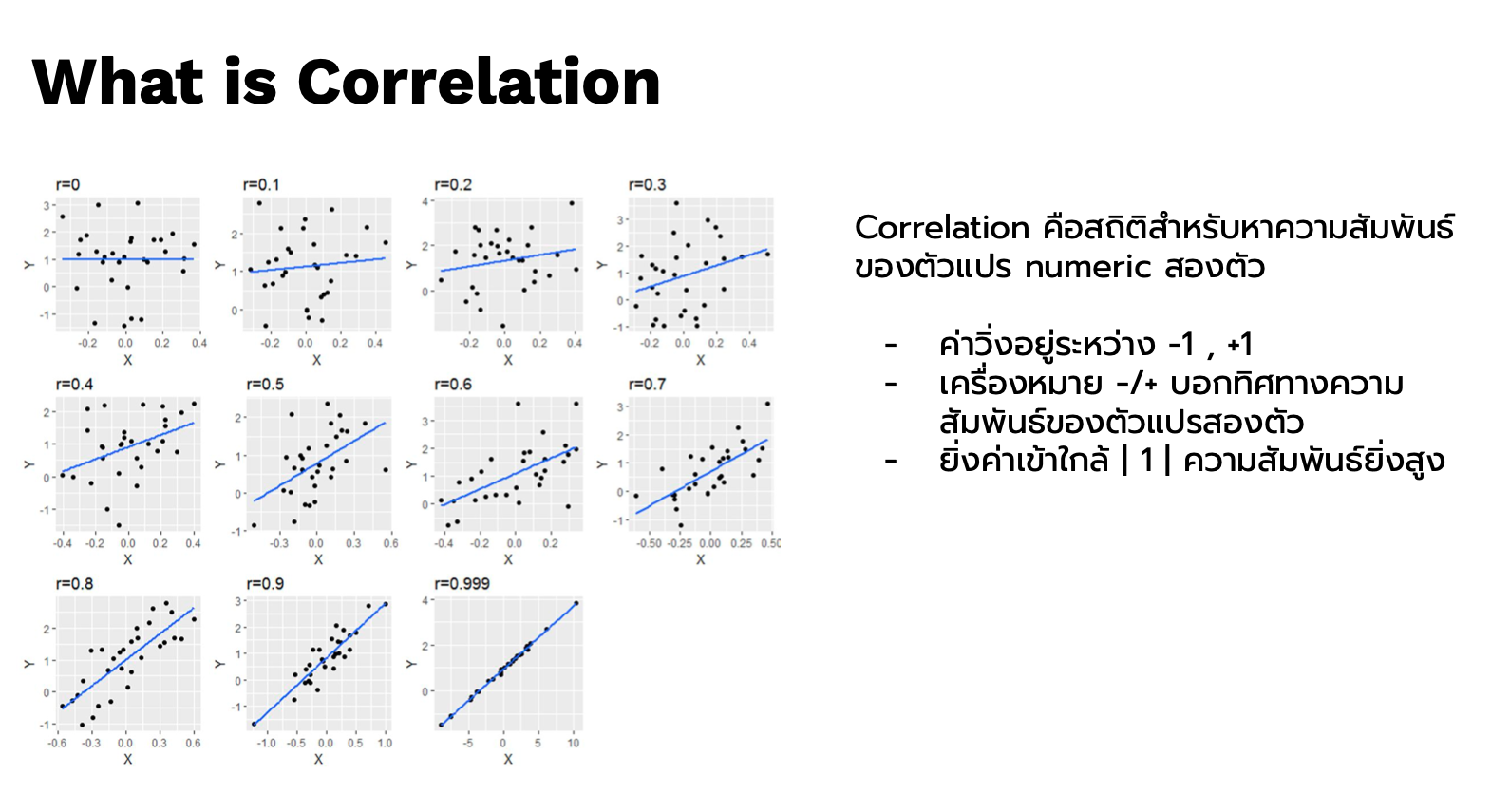
Correlation พื้นฐาน คือ Pearson Correleation ให้เกียรติแก่เพียร์สันในการคิดค้น
Correleation ใช้เมื่อไร
ใช้ในการวัดหาความสัมพันธ์ที่ตัวแปรเป็น Qualitative หรือ ตัวแปรที่เป็นตัวเลข 2 ตัว เช่น อายุ น้ำมัน แรงม้า
- ค่าจะวิ่งอยู่ +/- 1
- เครื่องหมาย +/- บอกทิศทางความสัมพันธ์ของตัวแปรสองตัว
- บวก มีทิศทางไปในทางเดียวกัน
- ลบ มีทิศทางตรงกันข้ามกัน
- ยิ่งค่าเข้าใกล้ Absolute 1 ความสัมพันธ์ยิ่งสูง ไม่ได้มีกฏตายตัวว่าเท่าไรจะเรียกว่าสูง เราจะกำหนดเป็น theshold ว่า 0.6-0.7 ถือว่าสูงก็ได้
- วัดความสัมพันธ์แบบเส้นตรง
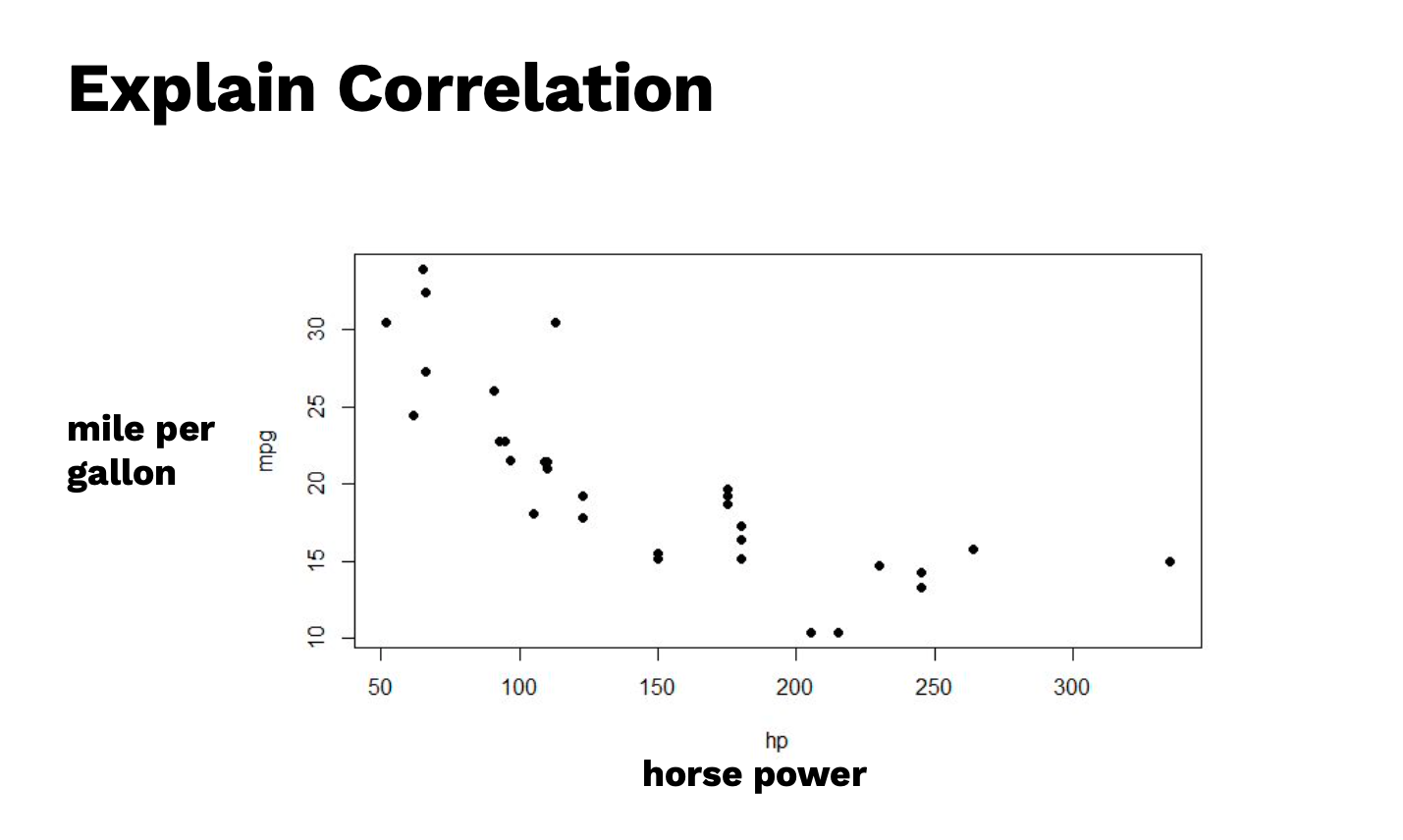
ถ้าสังเกตในกราฟ scatter plot ด้านบนนี้ จะเป็นแบบ Negative เพราะสังเกตว่าเมื่อตัวแปรต้นเพิ่มขึ้น ตัวแปรตามก็จะลดลง
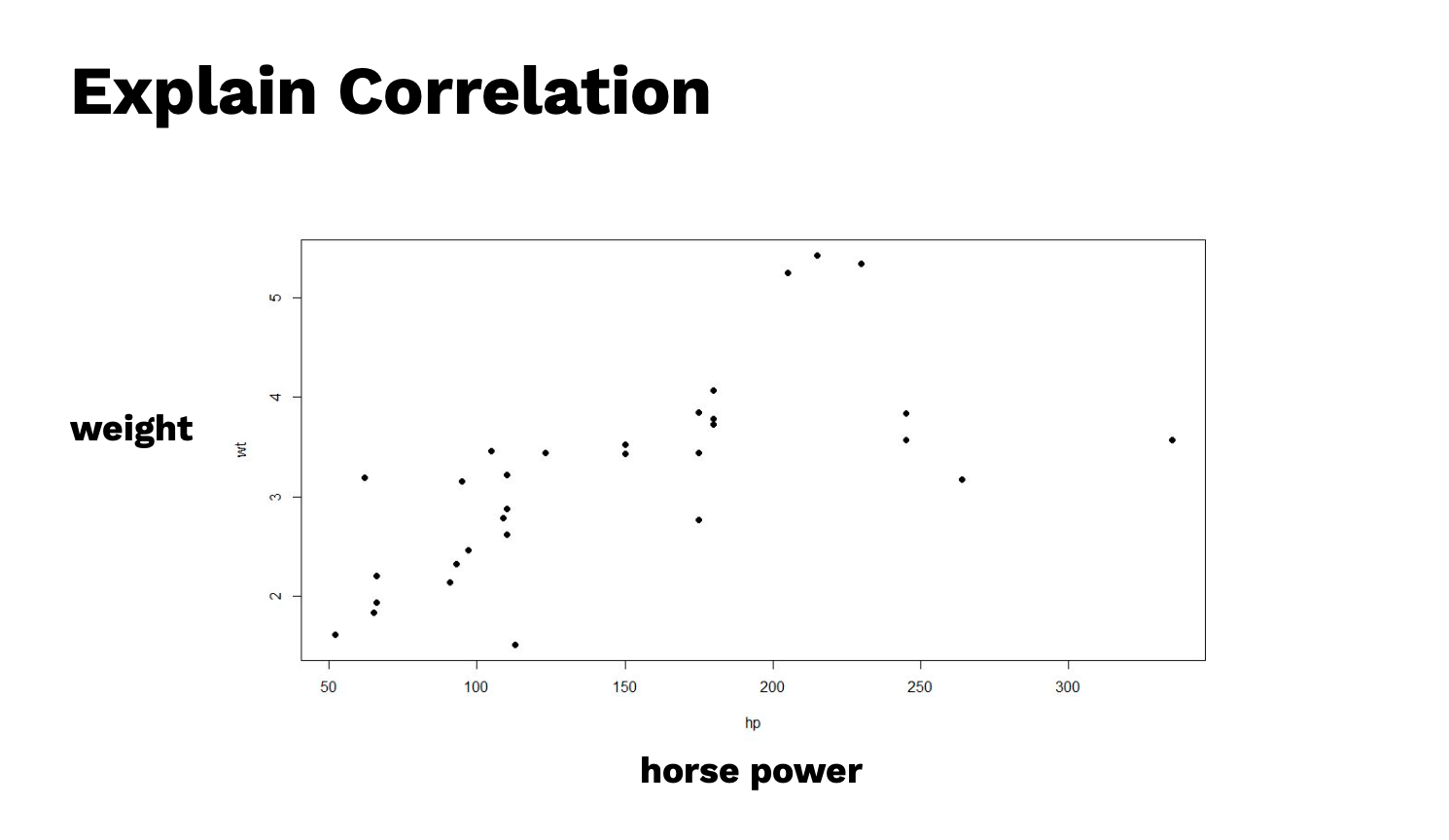
ลองเปลี่ยนตัวแปรตาม จะเป็นแบบ Positive เพราะสังเกตว่าเมื่อตัวแปรต้นเพิ่มขึ้น ตัวแปรตามก็จะเพิ่มขึ้น
ถ้าลองสังเกต ในตัวอย่างที่ผ่านมา สองตัว มันจะเป็นความสัมพันธ์แบบเส้นตรง แต่ถ้าสมมติว่า เมื่อไรก็ตามที่ความสัมพันธ์ไม่ใช่เส้นตรง Pearson Correleation จะไม่สามารถใช้งานได้ จะต้องใช้ สถิติที่สูงขึ้น
ให้เปิด Excel ด้วยไฟล์ mtcars ขึ้นมา
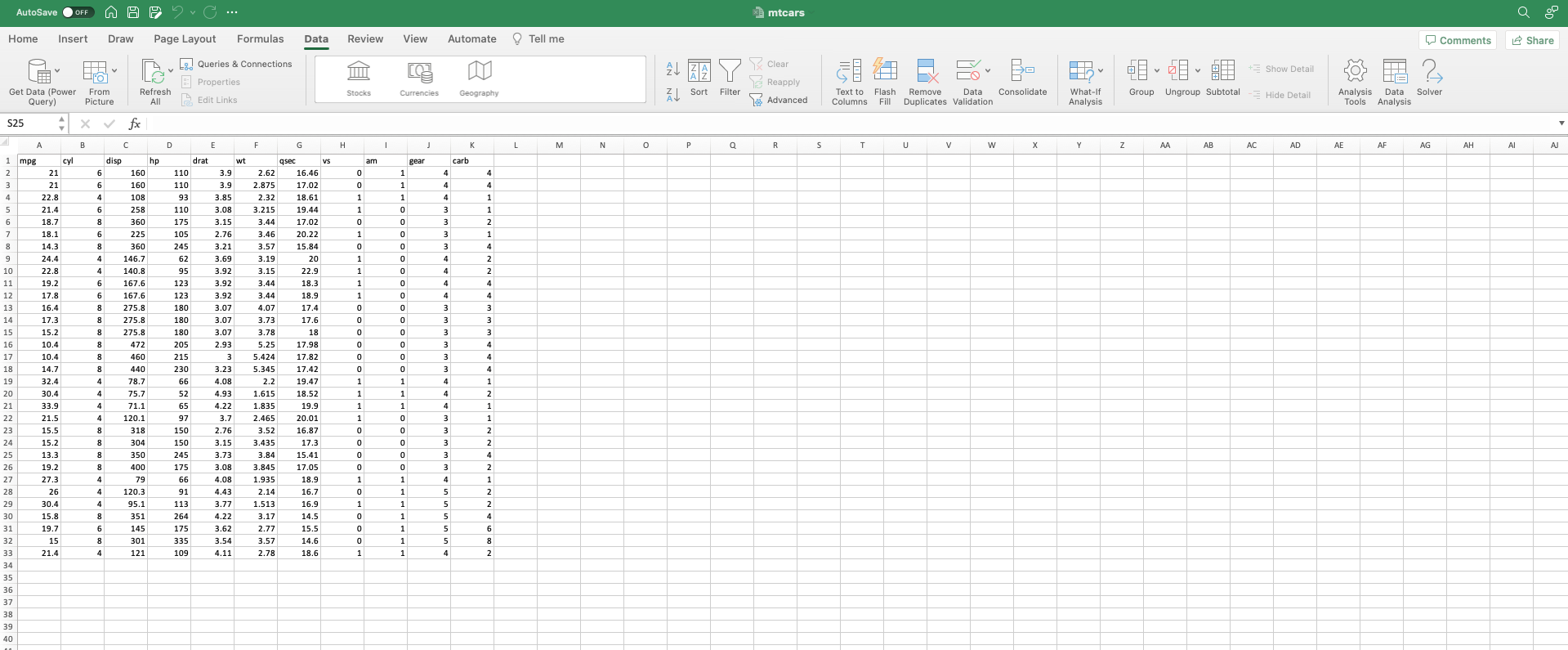
สมมติว่าเราอยากหา ค่าความสัมพันธ์ระหว่างคอลัมน์ mpg จะอยู่ที่ Column A กับ hp อยู่ที่ Column D โดยใช้สูตรหาความสัมพันธ์ Correlation โดยเลือกเฉพาะข้อมูล
=CORREL(A2:A33,D2:D33)
##
-0.776168372
จะเห็นว่าค่าที่ได้เท่ากับ -0.776168372
ถือว่ามีความสัมพันธ์ค่อนข้างสูง และ มีทิศทางตรงกันข้ามกันเพราะติดลบ
คราวนี้เราจะเอา ค่าใน column hp และ mpg มา plot graph เราก็จะได้กราฟหน้าตาแบบนี้ขึ้นมา
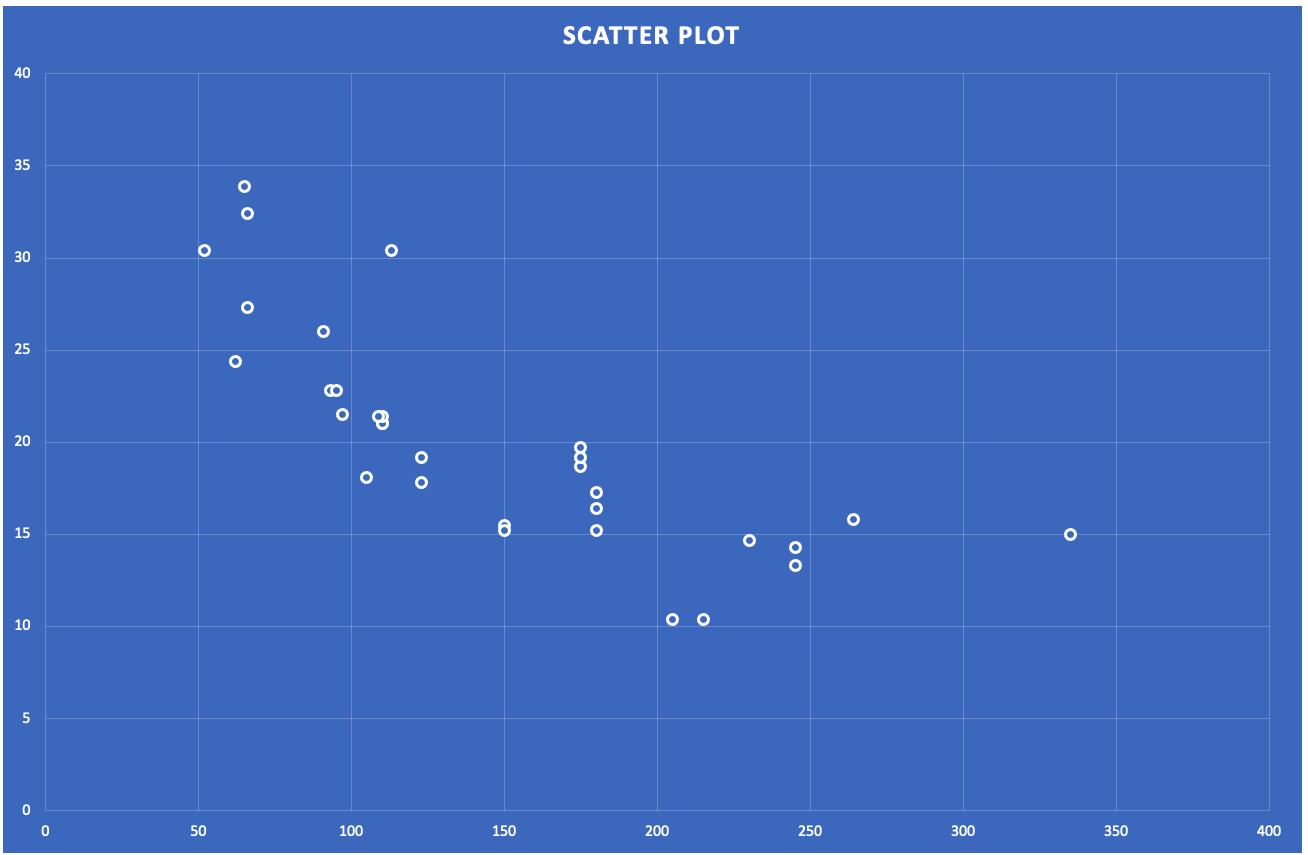
คราวนี้จะมาใช้ tool ตัวหนึ่งชื่อ data analysis toolpak ซึ่งจะต้อง download extension มาติดตั้งก่อน
หลังจากที่ติดตั้งเสร็จเรียบร้อยแล้ว ก็ไปที่ Tab Menu ชื่อ Data แล้วดูทางด้านขวามือจะมี ปุ่ม Data Analysis แล้วจะมี Dialog Tool ขึ้นมา ให้เลือก Tool ชื่อ Correlation
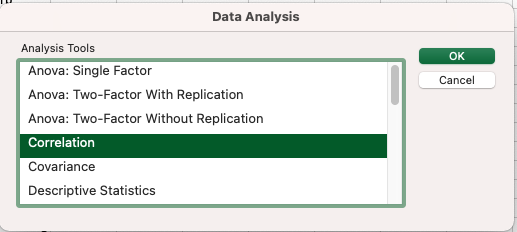
เลือก input ให้เลือก hp และ mpg ขึ้นมา และเลือก output ที่ cell ที่ต้องการจะวาง และอย่าลืม tick Labels in first row ถ้าข้อมูลในตารางมี header
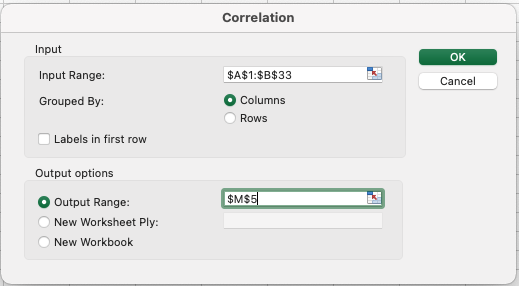
ผลลัพท์ที่เราได้
| hp | mpg | |
|---|---|---|
| hp | 1 | |
| mpg | -0.77617 | 1 |
ก็จะเห็นว่าค่าที่ได้ ก็จะเท่ากับที่เราคำนวนด้วย สูตรปกติ
ซึ่งเราสามารถที่จะหาความสัมพันธ์ชองข้อมูล mtcars ทั้งหมดได้เช่นเดียวกัน โดยเลือกทุก column
| hp | mpg | cyl | disp | drat | wt | qsec | vs | am | gear | carb | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| hp | 1 | ||||||||||
| mpg | -0.77617 | 1 | |||||||||
| cyl | 0.832447 | -0.85216 | 1 | ||||||||
| disp | 0.790949 | -0.84755 | 0.902033 | 1 | |||||||
| drat | -0.44876 | 0.681172 | -0.69994 | -0.71021 | 1 | ||||||
| wt | 0.658748 | -0.86766 | 0.782496 | 0.88798 | -0.71244 | 1 | |||||
| qsec | -0.70822 | 0.418684 | -0.59124 | -0.4337 | 0.091205 | -0.17472 | 1 | ||||
| vs | -0.7231 | 0.664039 | -0.81081 | -0.71042 | 0.440278 | -0.55492 | 0.744535 | 1 | |||
| am | -0.2432 | 0.599832 | -0.52261 | -0.59123 | 0.712711 | -0.6925 | -0.22986 | 0.168345 | 1 | ||
| gear | -0.1257 | 0.480285 | -0.49269 | -0.55557 | 0.69961 | -0.58329 | -0.21268 | 0.206023 | 0.794059 | 1 | |
| carb | 0.749812 | -0.55093 | 0.526988 | 0.394977 | -0.09079 | 0.427606 | -0.65625 | -0.56961 | 0.057534 | 0.274073 | 1 |
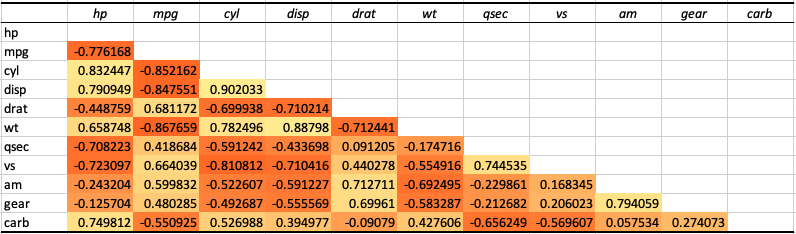
ถ้าลองสังเกตข้อมูลในตาราง วิธีการอ่าน
ถ้าความสัมพันธ์ระหว่าง row และ column มีความสัมพันธ์ในตัวมันเอง มันจะมีค่าเป็น 1
เราสามารถดูค่าความสัมพันธ์ระหว่าง hp กับตัวแปรอื่นๆ ได้
ช่องว่างๆ ที่เห็นด้านบนก็เป็นเพราะว่า มันสร้างความสัมพันธ์ไปแล้วที่ด้านล่าง
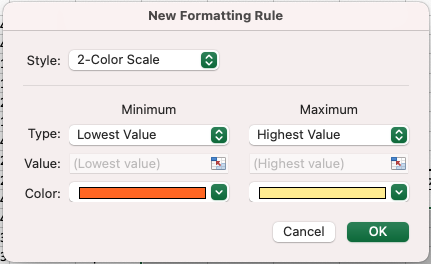
ให้เราลบเลข 1 ออกทั้งหมด จากนั้นเราจะเอาค่าที่ได้มาทำ heatmap เพื่อให้ดูง่ายขึ้นโดยไปที่เมนู Home แล้วเลือก Conditional Formatting
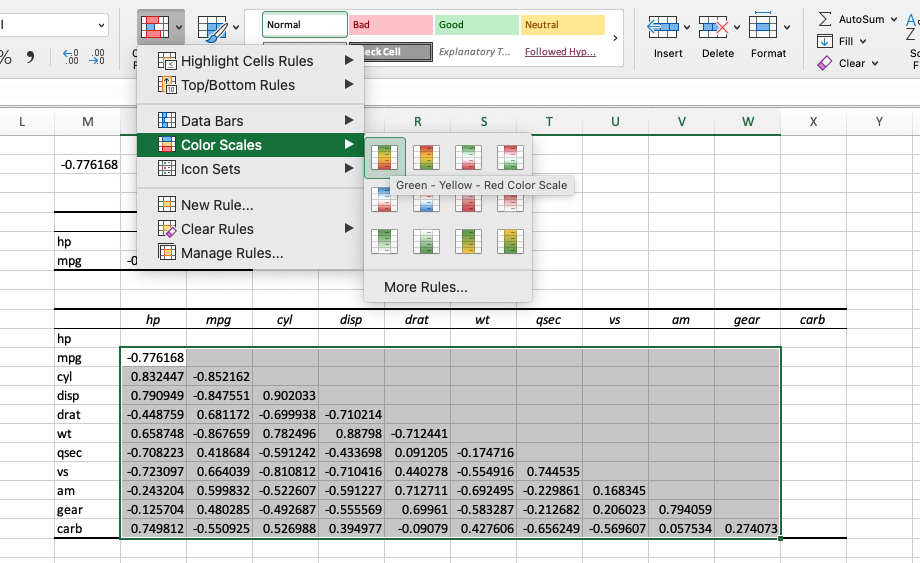
เลือก New Rule หรือ เลือก Rule ที่ excel เตรียมไว้ให้ก็ได้
คราวนี้มาดูนิยามของ Linear Regression คืออะไร
ข้อจำกัดของ Correlation มันบอกเราแค่ว่า ข้อมูลของเรามันเคลื่อนที่ในทิศทางเดียวกันหรือไม่ หรือ ความสัมพันธ์ สูงหรือต่ำ
ซึ่งมีอีกโมเดลที่ใช้ควบคู่ Correlation คือ Linear Regression
Linear Regression จะเป็นตัวช่วย วัดระดับความสัมพันธ์
หรือก็คือ เวลาที่เราหา Correlation ออกมาแล้วเห็นว่ามันมีความสัมพันธ์กัน ซึ่งคำถามถัดมาคือ เมื่อ x เปลี่ยนแปลง สมมติว่า 1 หน่วย แล้ว y จะเปลี่ยนเท่าไร
สมมติว่าจากตัวอย่าง
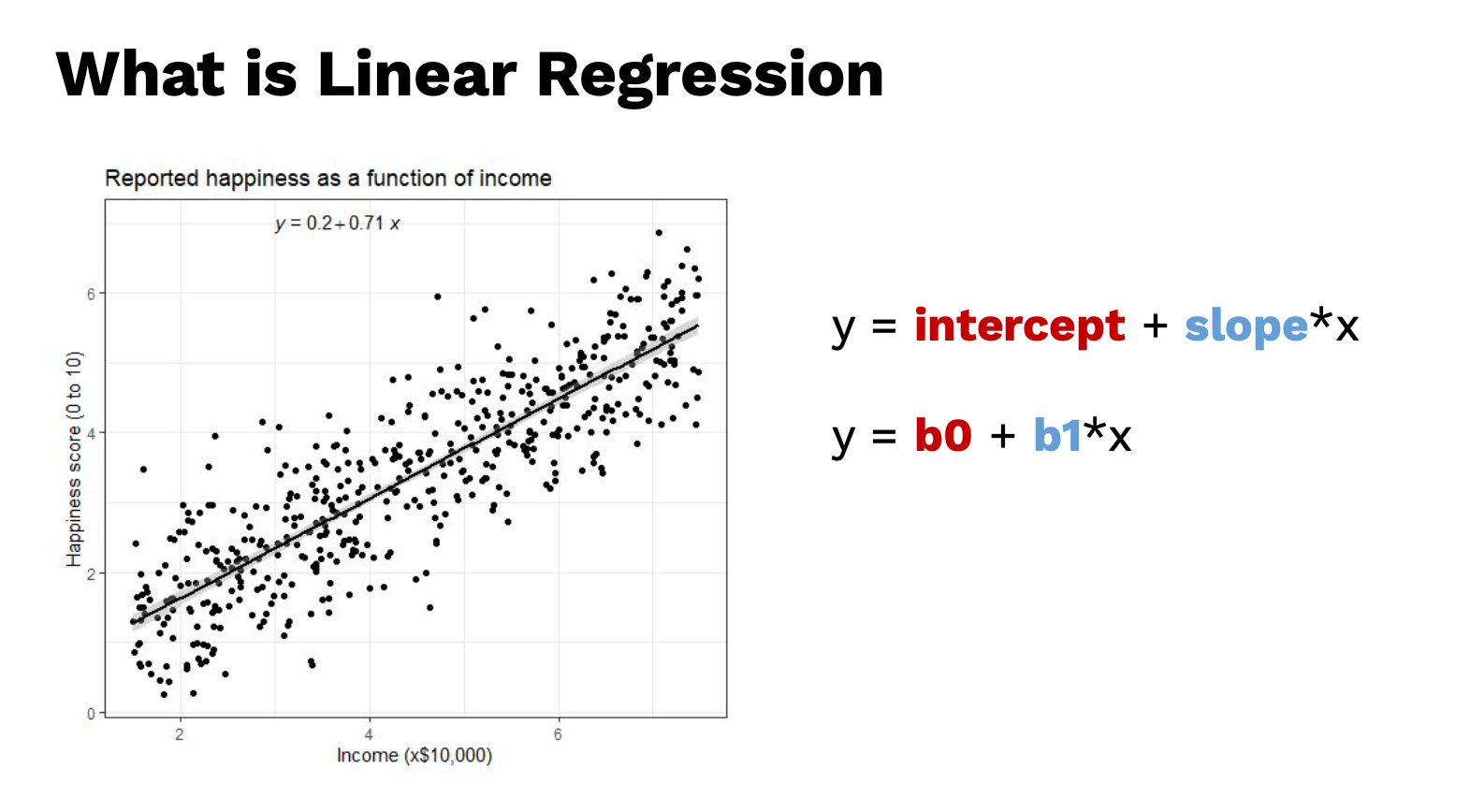
แกนนอน (x) เป็น income รายได้เงินเดือน หน่วยคูณด้วย $10k
แกนตั้ง happiness ความสุข มีค่า 1 ถึง 10
จะเห็นว่า เดือนเยอะขึ้น แล้ว ความสุขจะมากขึ้น แต่นี่คือตัวอย่าง อาจจะไม่จริงเสมอไป เป็นแค่ข้อมูล sample ถ้าข้อมูลเยอะกว่านี้ ความสุขอาจจะลดลงก็ได้ ซึ่งถ้า base on บนข้อมูลที่เห็นอยู่ในรูปภาพ ถ้าสมมติว่า จะทำนายคนที่มีเงินเดือน 2 ล้าน สมการนี้อาจจะไม่ตอบโจทย์
<aside> ???? ตัวอย่างนี้แสดงให้เห็นถึง เป็นข้อควรระวังว่าอย่า สรุปผลไปก่อนที่จะรู้ในส่วนอื่นๆ
</aside>
Model ของ Linear Regression คือ
y = intercept + slop*x
หรือ
y = b0 + b1*x
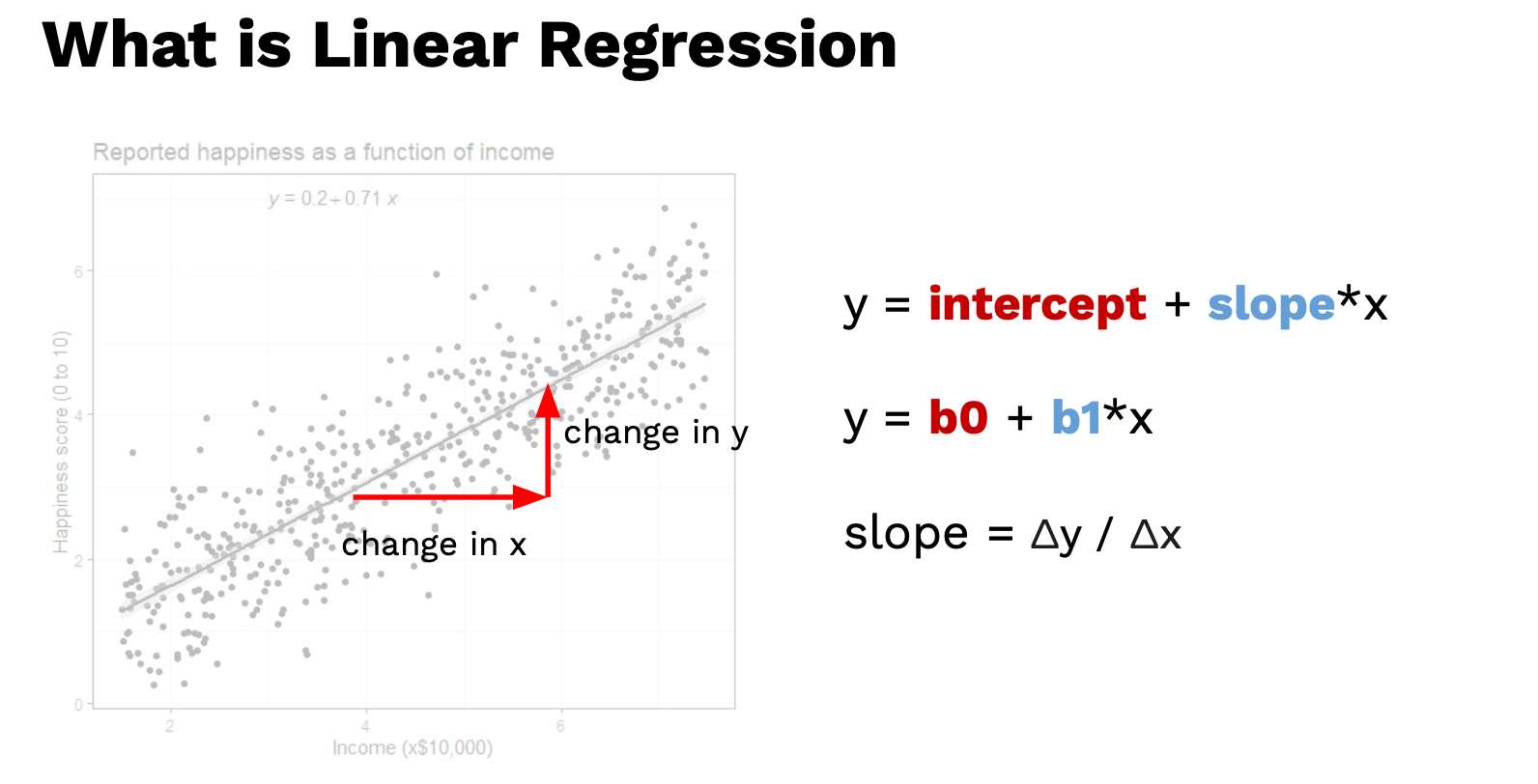
Slop เท่ากับ แกนตั้ง หารด้วย แกนนอน (rise over run)
การเปลี่ยนแปลงของ y หารด้วยการเปลี่ยนของ x
การเปลี่ยนแปลง x เปลี่ยนแปลงขึ้น 1 หน่วย ค่า y จะเปลี่ยนแปลงเท่าไร
ก็จะเห็นว่า correlation กับ linear regression มันมีความสัมพันธ์กันอยู่
เราสามารถมองว่า slop คือ ค่า correlation ก็ได้
ถ้าสังเกตค่า slop จะมีค่าน้อยกว่าหนึ่ง เพราะว่า change in y มันเล็กกว่า change in x ซึ่ง ดูขนาดอัตราส่วนได้
มาดูคำถามถัดมา ถ้าดูจากรูปที่ผ่านมา เรารู้ได้อย่างไรว่า สามารถใช้เส้นตรงเส้นที่ plot อยู่นี้ได้ ให้ลองคิดดูว่า จริงๆแล้ว จุดข้อมูลบนกราฟมีเยอะมาก ค่า slop จะเป็นเท่าไรก็ได้
ซึ่งคำตอบก็คือ เส้นตรงเส้นนี้ จะถูกเรียกว่า เส้นตรงที่ดีที่สุด The best of line
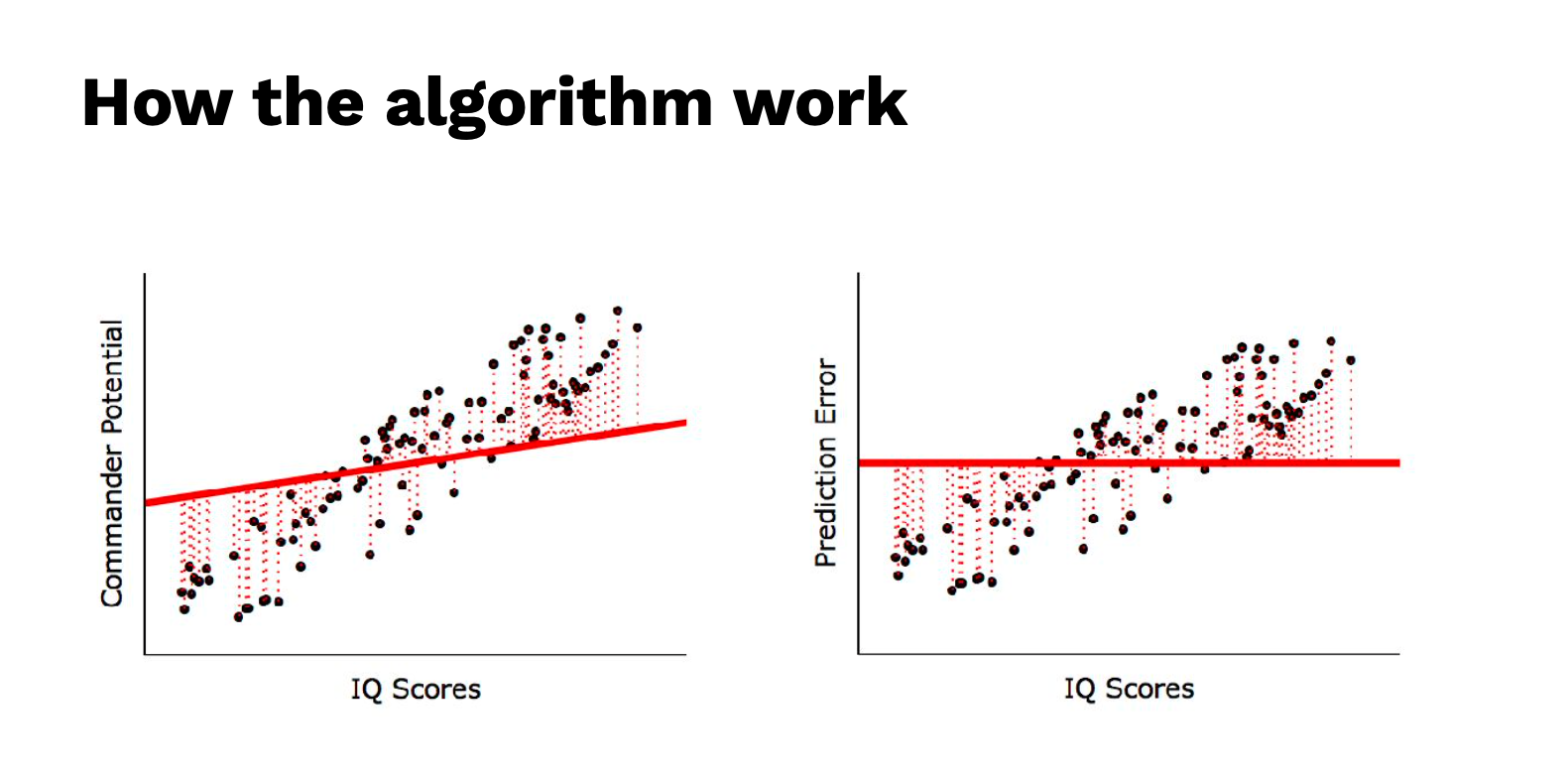
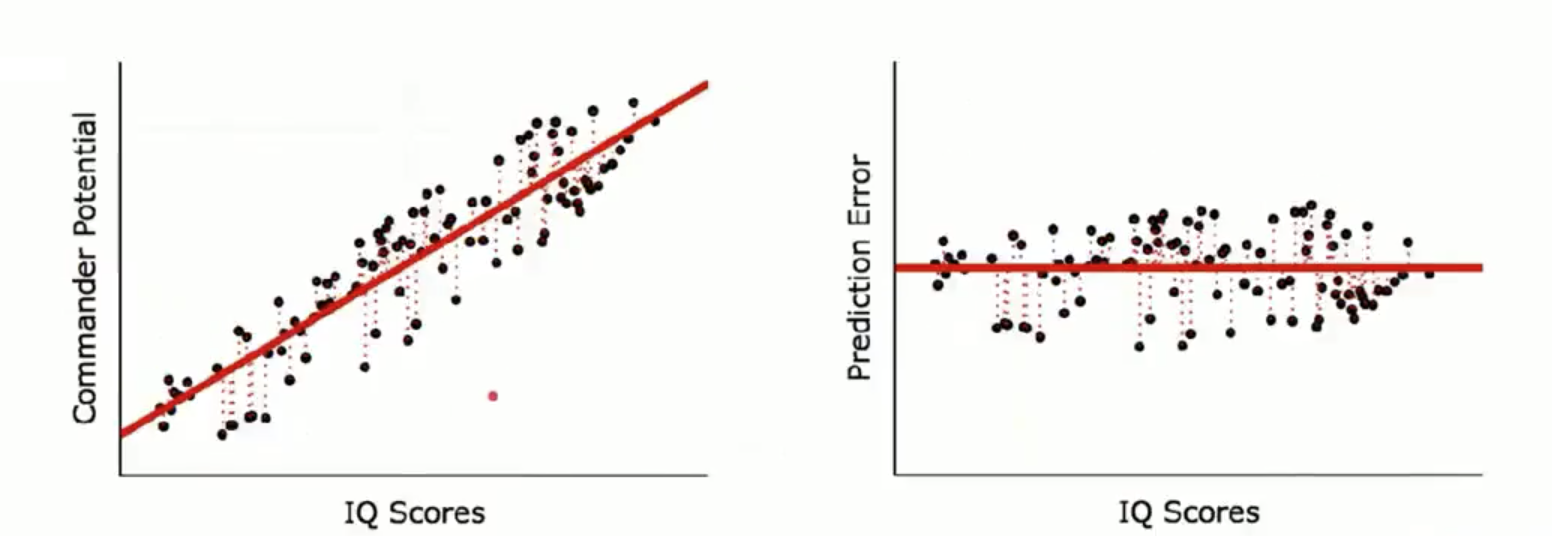
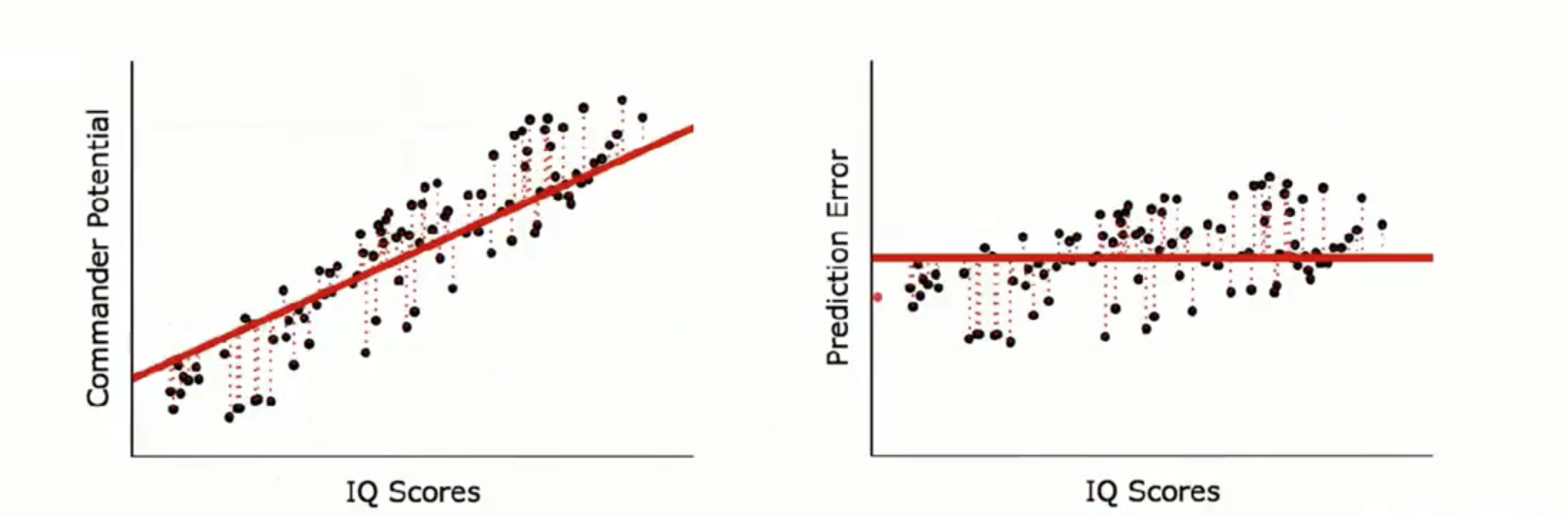
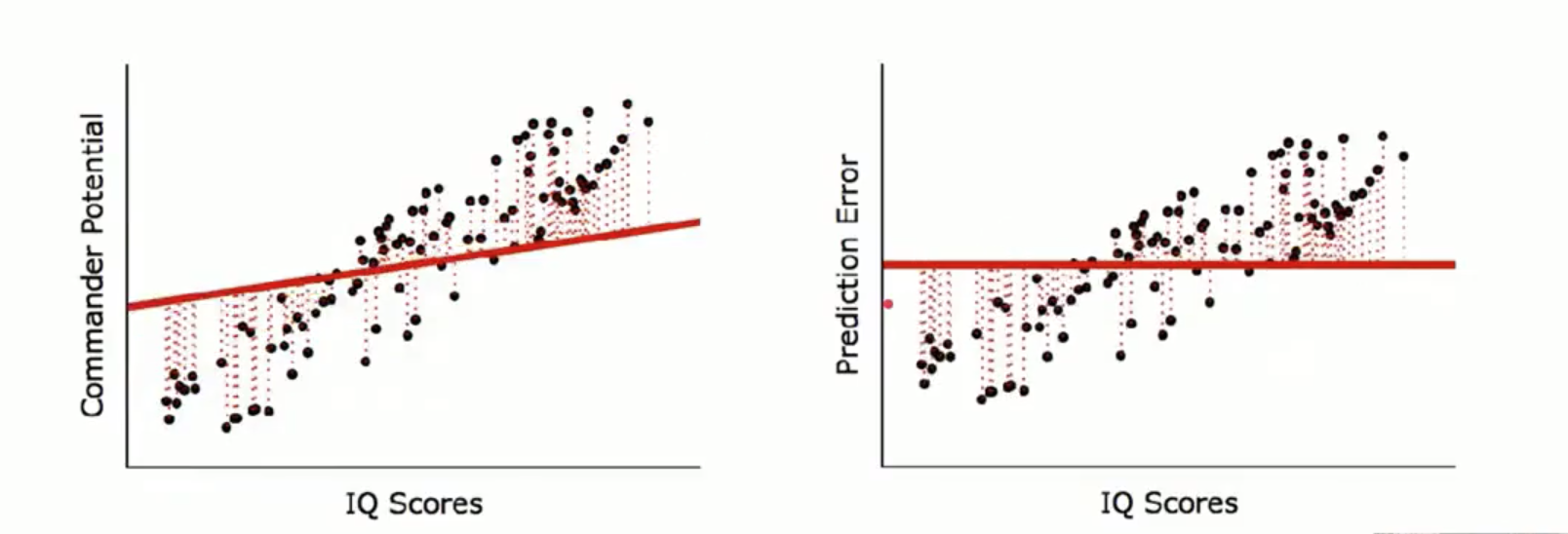
รูปทางซ้ายมือจะเป็น สมการ Regression ส่วน ภาพทางด้านขวา เป็น Pridiction Error
ภาพทางด้านซ้ายจะภาพทั้ง 3 ภาพไล่เรียงลงมา จะเห็นว่ามีเส้นปะ ของจุดแต่ละจุด ซึ่งเป็นตัวที่บอกว่า เส้นสมการมีค่า Error น้อยที่สุด สังเกตว่าเส้นปะน้อยตามไปด้วย
ภาพทางด้านขวา เป็นการดูค่า error ที่น้อยที่สุดก็คือ จุดสีดำ เข้าใกล้แกน Zero มากเท่าไร นั้นคือ Error น้อยที่สุด
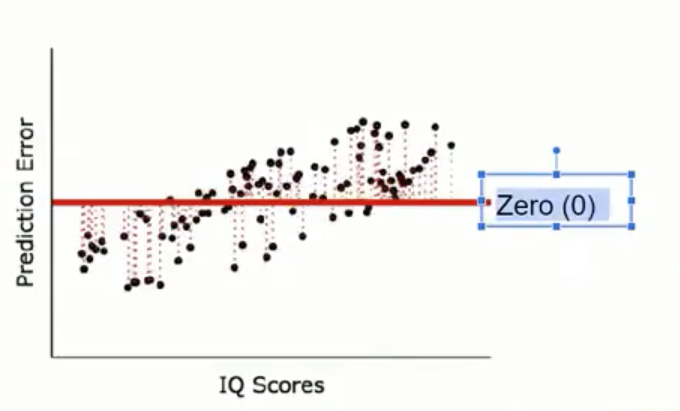
คราวนี้มาดูภาพนี้ครับ ภาพนี้คือ เส้นตรงที่ดีที่สุด และ ได้ error ต่ำที่สุด
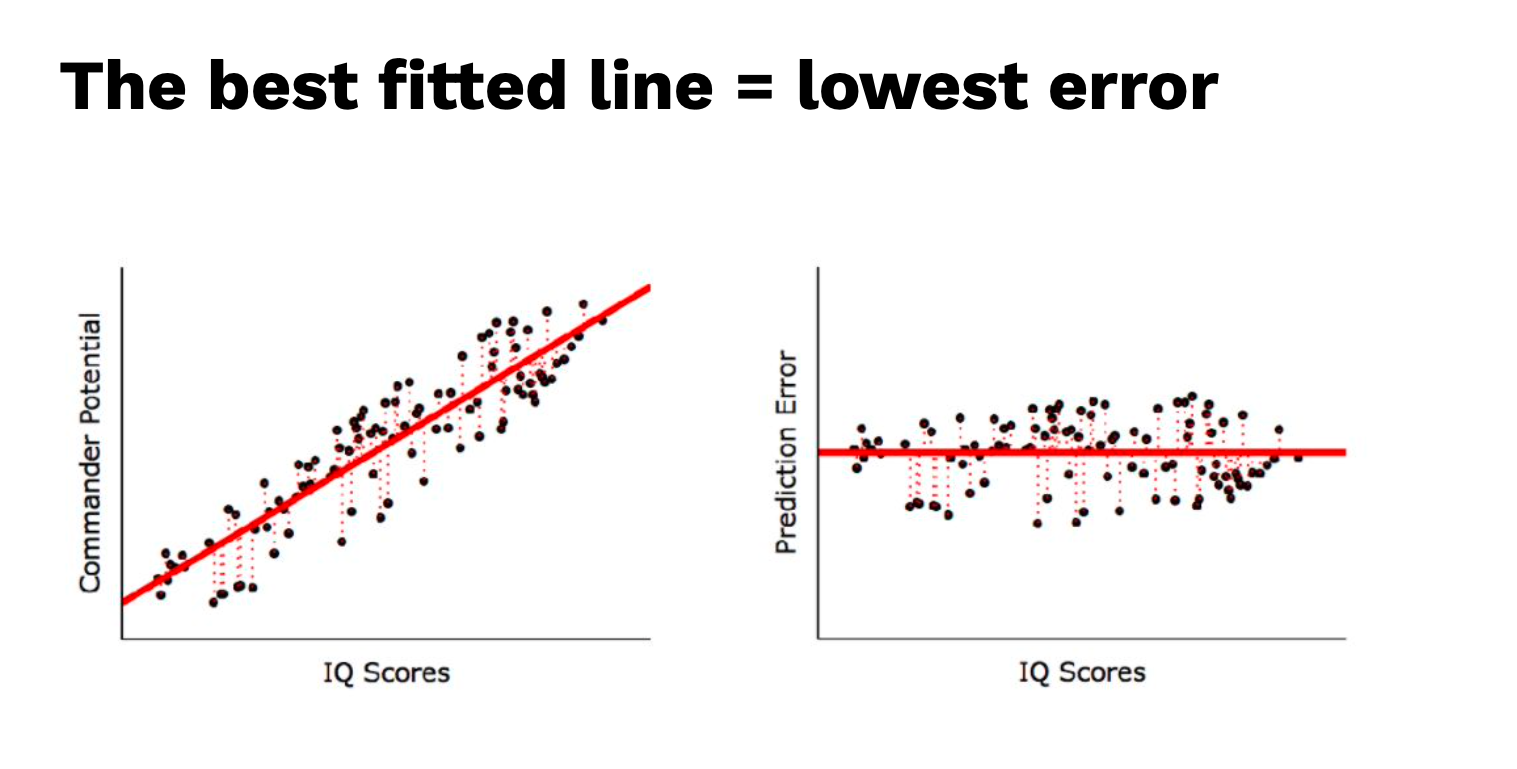

- HP เป็นตัวแปรต้น MPG เป็นตัวแปรตาม
- Correlation เป็น Negative
- MPG จะเท่ากับ 30.09
- MPG จะเท่ากับ 18.09
ลองกลับมาที่ Excel
b0 จะเรียกว่า intercept เป็นค่าจุดเริ่มต้นความชัน
b1 ก็คือ ค่าความชัน หรือ slope
ใน excel สามารถหาได้ด้วย สูตร =INTERCEPT และ =SLOPE ตามตารางตัวอย่างด้านล่างได้เลย
| mpg | hp | ||||
|---|---|---|---|---|---|
| 21 | 110 | ||||
| 21 | 110 | mpg = f(hp) | |||
| 22.8 | 93 | mpg = b0 + b1*hp | |||
| 21.4 | 110 | ||||
| 18.7 | 175 | ||||
| 18.1 | 105 | ||||
| 14.3 | 245 | intercept | 30.09886054 | =INTERCEPT(A2:A33,B2:B33) | |
| 24.4 | 62 | Slope | -0.068228278 | =SLOPE(A2:A33,B2:B33) | |
| … | … |
เรามาลองใช้ Toolpak หาผลสรุป ข้อมูล mtcars นี้กัน
เมื่อเปิด Data Analysis ขึ้นมาแล้ว ก็เลือก Regression

ใส่ input X, Y และ เลือก Output
มันจะสรุปผลโดยที่เราไม่ต้องเขียนสูตรเลย
| SUMMARY OUTPUT | ||||||||
|---|---|---|---|---|---|---|---|---|
| Regression Statistics | ||||||||
| Multiple R | 0.776168372 | |||||||
| R Square | 0.602437341 | |||||||
| Adjusted R Square | 0.589185253 | |||||||
| Standard Error | 3.862962221 | |||||||
| Observations | 32 | |||||||
| ANOVA | ||||||||
| df | SS | MS | F | Significance F | ||||
| Regression | 1 | 678.372874 | 678.372874 | 45.4598033 | 1.7878E-07 | |||
| Residual | 30 | 447.6743135 | 14.9224771 | |||||
| Total | 31 | 1126.047188 | ||||||
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | Lower 95.0% | Upper 95.0% | |
| Intercept | 30.09886054 | 1.63392095 | 18.4212465 | 6.6427E-18 | 26.7619488 | 33.4357723 | 26.7619488 | 33.4357723 |
| X Variable 1 | -0.068228278 | 0.010119304 | -6.7423885 | 1.7878E-07 | -0.0888947 | -0.0475619 | -0.0888947 | -0.0475619 |
เราจะมาลองอ่านค่าผลสรุปของแต่ละตัว
ให้สังเกตค่า Coefficients จะได้ค่าที่เท่ากับ ค่าที่ใช้สูตร intercept กับ slope ทางด้านบนเขียนเอาไว้
ค่า R Sqrt (R Square 0.602437341)
ใช้ในการวัดผลของ Model โดยจะมีค่าที่วิ่งอยู่ที่ 0 ถึง 1
ยิ่งเข้าใกล้ 1 มากเท่าไร ก็จะยิ่งสามารถอธิบาย ค่า hp หรือ ค่าความชัน ได้มากเท่านั้น
อย่างตัวอย่างนี้ คือ hp สามารถอธิบาย mpg (mile per gallon) ได้ถึง 60.2%
ถ้าเท่ากับ 1 แสดงว่า มันมีความสัมพันธ์ที่อธิบายได้ 100%
ยิ่งเข้าใกล้หนึ่ง Model ของเรานั้นดีมาก ตรงกันข้าม ยิ่งเข้าใกล้ศูนย์ Model เราไม่ค่อยดี
ค่า Correlation (Multiple R 0.776168372)
| Multiple R | 0.776168372 |
|---|---|
| R Square | 0.602437341 |
| Adjusted R Square | 0.589185253 |
| Standard Error | 3.862962221 |
| Observations | 32 |
ค่า R Sqrt จริงๆแล้ว มันเกิดมาจากค่า Correlation
ลองใช้ สูตร CORREL ใน Excel แล้วเลือก mpg , hp
=CORREL(B2:B33,A2:A33)
##
-0.776168372
จะเห็นว่า มีค่าเท่ากัน
แล้วค่า R Sqrt ก็คือ ค่า Correlation ที่ยกกำลังสอง
=-0.776168372^2
##
0.602437341
R Sqrt เรียกอีกอย่างหนึ่งในทางสถิติว่า Explain Variances ซึ่งแปลว่า ค่าความแปรปรวนของตัวแปรทั้งสองตัว มันอธิบายกันได้กี่เปอร์เซ็น หรือ ตัวแปร x อธิบายความแปรปรวนของ ตัวแปร y ได้ทั้งหมด 60.2%
ANOVA
ค่า Anova จะเรียกอีกอย่างว่า Overall Significance of the model
| ANOVA | |||||
|---|---|---|---|---|---|
| df | SS | MS | F | Significance F | |
| Regression | 1 | 678.372874 | 678.372874 | 45.4598033 | 0.0000 |
| Residual | 30 | 447.6743135 | 14.9224771 | ||
| Total | 31 | 1126.047188 |
Significance F ค่า p-value
0.0000
*< 0.05
ถ้าค่านี้มีค่าน้อยกว่า 0.05 เราจะสรุปผลว่า Significance หมายถึง ตัวแปร X สามารถอธิบาย ตัวแปร Y ได้อย่างมีนัยสำคัญทางสถิติ
เราสามารถที่จะสรุปผลได้ว่า ค่าแรงม้า (hp) สามารถทำนาย Mile per gallon ได้อย่างมีนัยสำคัญทางสถิติ อยู่ที่ความสัมพันธ์ 60.2%
Coefficients ค่าสัมประสิทธิ์โมเดล
ถ้าจาก สมการ model หน้าตาของตัวอย่างจะเป็นแบบนี้
mpg = 30.10 + (-0.07)*hp
เราสามารถที่จะทดสอบ significance ของค่าสัมประสิทธิ์แต่ละตัวได้
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept | 30.09886054 | 1.63392095 | 18.4212465 | 6.6427E-18 | 26.76194879 | 33.4357723 |
| X Variable 1 | -0.068228278 | 0.010119304 | -6.7423885 | 1.7878E-07 | -0.088894654 | -0.0475619 |
ที่ column p-value ให้เปลี่ยนค่ายกกำลัง เป็นทศนินม 4 ตำแหน่ง โดยกด commas
P-value
0.00
0.00
ก็จะเห็นว่าค่า hp สามารถ อธิบายได้อย่างมีนัยสำคัญทางสถิติเช่นเดียวกัน
มีจุดสังเกตอยู่นิดนึงสำหรับตัวอย่างนี้
ให้กลับมาดูที่ สมการโมเดลของเรา แล้วสมมติว่า hp มีค่าเป็น 0 ให้ลองนึกดูว่า ในความเป็นจริง hp เป็น 0 ไม่มีแรงม้า แสดงว่าจริงๆแล้ว รถไม่เคลื่อนที่ แล้วมันจะมีแรงม้าได้อย่างไร
mpg = 30.10 + (-0.07)*hp
สิ่งที่ต้องระวัง เป็นข้อจำกัน ในค่าของ intercept ซึ่งนักสถิติ จะสนใจค่าความชันมากกว่า
Confidence Interval
| Lower 95% | Upper 95% |
|---|---|
| 26.76194879 | 33.4357723 |
| -0.088894654 | -0.0475619 |
ค่า Observation คือจำนวนรถยนต์มีทั้งหมด 32 คัน
ค่าความเชื่อมั่น สมมติว่าเรามีการสุ่มตัวอย่างขึ้นมาใหม่ ในทุกๆครั้ง ค่า hp กับค่า intercept ก็จะเปลี่ยนไปเรื่อยๆ จริงๆแล้วเราสนใจแค่ค่า hp ซึ่ง เราสุ่มใหม่ไปเลย 100 ครั้ง ใน 95% ค่า ของ hp จะเปลี่ยนแปลงอยู่ในช่วง -0.088894654. จนถึง -0.0475619 โดยเราเชื่อมั่นที่ 95% มั่นใจที่ 95% เท่านั้น

ตัวอย่างที่ผ่านมาเป็น linear regression เพียง 1 ตัวแปร แต่ในชีวิตจริง มันไม่ได้มีตัวแปรเพียงแค่ตัวเดียว มันมีมากกว่า 1 ตัว หรือเป็น multiple linear regression ซึ่งจะเป็นไปตาม สมการที่สอง ในรูปภาพด้านบน
มาลองทำ multiple linear regression กัน โดยใช้ data set เดียวกัน คือ mtcars แต่คราวนี้จะมีหลาย column โดย column ที่จะมาทดลองสร้าง model จะมี hp, wt, am, และ ตัวแปรตาม ก็คือ mpg เหมือนเดิม
| hp | wt | am | mpg |
|---|---|---|---|
| 110 | 2.62 | 1 | 21 |
| 110 | 2.875 | 1 | 21 |
| 93 | 2.32 | 1 | 22.8 |
| 110 | 3.215 | 0 | 21.4 |
| 175 | 3.44 | 0 | 18.7 |
| … | … | … | … |
ทั้งหมดจะมี 32 คัน แต่จากตารางเอาแสดง 5 แถว
จากสมการโมเดล multiple linear regression
mpg = f(hp, wt, am)
mpg = b0 + b1*hp + b2*wt + b3*am
เราสามารถใช้สูตรชื่อว่า Linest มาสร้างค่าสัมประสิทธิ์ของแต่ละตัวได้
โดยเลือก y ซึ่งจะเป็น mpg คือ output ที่อยากให้ทำนาย
และ x จะมีอยู่ 3 ตัว คือ hp, wt, am
=LINEST(D2:D33,A2:C33)
ได้ผลลัพท์
| am | wt | hp | intercept |
|---|---|---|---|
| 2.08371013 | -2.8785754 | -0.0374787 | 34.0028751 |
คราวนี้เราลองมาใช้ analysis toolspak ทำเพื่อเทียบค่ากัน โดยจริงๆแล้วสูตรนี้ไม่จำเป็นต้องทำก็ได้เพราะใช้ toolpak ก็ใช้ได้เลย
เลือก column แบบหลาย column ได้เลยใน Input X Range
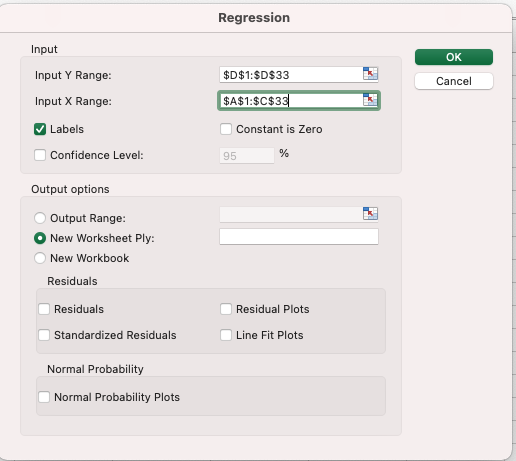
เราก็จะได้ข้อมูลสรุปออกมา
| SUMMARY OUTPUT | |||||
|---|---|---|---|---|---|
| Regression Statistics | |||||
| Multiple R | 0.91645529 | ||||
| R Square | 0.83989031 | ||||
| Adjusted R Square | 0.82273569 | ||||
| Standard Error | 2.53751194 | ||||
| Observations | 32 | ||||
| ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 3 | 945.756116 | 315.252039 | 48.9600345 | 2.9079E-11 |
| Residual | 28 | 180.291072 | 6.43896685 | ||
| Total | 31 | 1126.04719 | |||
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | |
| Intercept | 34.0028751 | 2.64265934 | 12.8669158 | 2.824E-13 | 28.5896329 |
| hp | -0.0374787 | 0.00960542 | -3.9018302 | 0.0005464 | -0.0571545 |
| wt | -2.8785754 | 0.90497054 | -3.1808499 | 0.00357403 | -4.7323235 |
| am | 2.08371013 | 1.37642015 | 1.51386198 | 0.14126824 | -0.7357587 |
เรามาดู Column ชื่อ am สักนิด เพราะว่ามันมีค่าเป็น 0 กับ 1 ซึ่งปกติจะเรียนข้อมูลของ column แบบนี้ว่า dummy หรือ indicator ซึ่ง 0 ในตารางนี้ คือ เกียร์ Auto และ 1 เกียร์ Manual
ถ้าเราต้องการแค่ค่าสัมประสิทธิ์ เราก็ใช้แค่สูตร Linest ก็ได้ แต่ถ้าต้องการข้อมูลสรุป ใช้ toolpak ดีกว่า
คราวนี้มาพิจารณาเหมือนกับ simple linear regression กัน
R Square
| Multiple R | 0.91645529 |
|---|---|
| R Square | 0.83989031 |
| Adjusted R Square | 0.82273569 |
| Standard Error | 2.53751194 |
| Observations | 32 |
ค่า R Square ถ้าเข้าใกล้ 1 ก็จะถือว่าดี สามารถที่จะอธิบายค่า Variant ได้ถึง 83.9% ลองพิจารณาดู จะเห็นว่ามากกว่าแบบ Simple Linear Regression
ในการที่เราใส่ตัวแปร X หลายๆ ตัว มันจะเหมือนกับการที่เอาตัวแปรมาช่วยกันทำนาย ว่า MPG น่าจะเป็นเท่าไร
ซึ่งถ้าลองพิจารณาตาม common sense แล้ว ตัวแปรที่เลือกมาก็น่าจะมีส่วนเกี่ยวข้องที่จะทำให้ตัวแปร Y หรือ. MPG ของเรานี้มีการเปลี่ยนแปลง ซึ่งตัวอย่างนี้ก็ทำให้สูงขึ้นเป็น 83.9%
Anova
| ANOVA | |||||
|---|---|---|---|---|---|
| df | SS | MS | F | Significance F | |
| Regression | 3 | 945.756116 | 315.252039 | 48.9600345 | 0.0000 |
| Residual | 28 | 180.291072 | 6.43896685 | ||
| Total | 31 | 1126.04719 |
ให้ลองสังเกตที่ Signigicance จะเห็นว่ามีค่าน้อยกว่า p-value ซึ่งก็คือ 0.05 มันแปลได้ว่า มีนัยสำคัญทางสถิติ ซึ่ง ในที่นี้ มันจะหมายถึง มีตัวแปรใดตัวแปรหนึ่ง ที่เป็นตัวแปรต้น ใน 3 ตัว ที่นำมาใช้อย่างน้อย 1 ตัวที่สามารถทำนาย MPG ได้ ซึ่งอีกความหมายหนึ่ง ไม่ได้ความว่า ในตัวแปรต้นทั้ง 3 ตัว ไม่ได้จะมีนัยสำคัญทางสถิติทุกตัว โดยที่จะต้องไปดูในตารางถัดไป ก็คือ ตารางค่าสัมประสิทธิ์
Coefficients
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept | 34.0028751 | 2.64265934 | 12.8669158 | 0.0000 | 28.5896329 | 39.4161174 |
| hp | -0.0374787 | 0.00960542 | -3.9018302 | 0.0005 | -0.0571545 | -0.0178029 |
| wt | -2.8785754 | 0.90497054 | -3.1808499 | 0.0036 | -4.7323235 | -1.0248273 |
| am | 2.08371013 | 1.37642015 | 1.51386198 | 0.1413 | -0.7357587 | 4.903179 |
ย้อนกลับมาดูสมการ กันก่อน เราสามารถใส่ค่าสัมประสิทธิ์ลงไปในสมการได้เลย
mpg = f(hp, wt, am)
mpg = b0 + b1*hp + b2*wt + b3*am
mpg = 34.0029 + (-0.03)*hp + (-2.87)*wt + 2.08*am
ถ้าสมมติว่า
hp = 200
wt = 3.5
am = 1
คำถามคือ ค่า mpg จะมีค่าเท่าไร
ลองคำนวนดูใน excel
| Coefficients | |
| Intercept | 34.0028751 |
| hp | -0.0374787 |
| wt | -2.8785754 |
| am | 2.08371013 |
| hp | 200 |
| wt | 3.5 |
| am | 1 |
| predicted mpg | 18.5158261 |
โดยใส่ค่าตามสมการ
=G26+G27*G31+G28*G32+G29*G33
ย้อนกลับมาที่ตารางค่าสัมประสิทธิ์ ค่า p-value สักนิดนึง
| P-value | |
|---|---|
| Intercept | 0.0000 |
| hp | 0.0005 |
| wt | 0.0036 |
| am | 0.1413 |
จะเห็นว่าจะมีอยู่ค่าหนึ่ง ก็คือ am ที่ไม่ significance เพราะมีค่า น้อยกว่า 0.05 ดังนั้นค่า hp กับ wt มีนัยสำคัญทางสถิติ ซึ่ง เราสามารถตัด column นั้นทิ่งไปก็ได้ ถ้า column นั้นไม่ significance แต่ในทางตรงกันข้าม am คือประเภทของเกียร์ ให้ลองนึกถึงความเป็นจริง เกียร์ auto กับ manual มีผลการบริโภคน้ำมันหรือไม่
ก็อาจจะมีก็ได้
ดังนั้นการที่ค่า am ไม่ significance ก็อาจจะเป็นไปได้ว่า เราสุ่มตัวอย่างหรือเก็บข้อมูลไม่มากพอ ในตัวอย่างนี้มีจำนวนตัวอย่างอยู่ 32 คัน มันน้อยเกิดไป ซึ่งถ้าเราเก็บมากกว่านี้ อาจจะ 500 คัน ขึ้นไป am อาจจะมีผลและเกิดค่าที่มีนัยสำคัญทางสถิติก็ได้ โดยในเรื่องนี้สามารถสรุปได้ว่า ค่าต่างทางสถิติและค่า p-value ขึ้นอยู่กับ sample size ด้วย
การคำนวนหรือขั้นตอนการทำ data analysis ด้วย toolpak ที่ผ่านมา สมมติว่า แค่อยากจะทำนายค่า Y เราไม่จำเป็นต้องดู p-value ก็ได้
Objective for Run Model : วัตถุประสงค์ของการวิเคราะห์นี้มีอยู่ 2 อย่าง
- การทำนายผลค่า Y (Pridicted)
- ทำสร้างโมเดลขึ้นมาเพื่อทำนายเพียงอย่างเดียว อย่างเช่น พวก Deep Learning มันเป็นเหมือนกับ Black box ที่ไม่สามารถอธิบายตัวแปรต่างๆที่อยู่ภายในได้ แต่มันแม่นยำมากในการทำนาย ซึ่งเกิดมาเพื่อทำนายที่ดี
- การวิเคราะห์ Inference Y เป็นการดูค่าแต่ละตัวว่าเกิดอะไรขึ้นกับตัวแปรต้น X สามารถที่จะปรับจูนค่าต่างๆให้ Y ดีขึ้น แต่การทำ Inference model แบบนี้ Performance ในการทำนายที่ไม่ค่อยดีเท่าไร
คราวนี้เราจะมาทำนายค่า mpg ด้วยสมการนี้กัน
mpg = 34.0029 + (-0.03)*hp + (-2.87)*wt + 2.08*am
โดยสร้าง column ใหม่ขึ้น 1 column แล้วใช้ excel ในการคำนวนเมื่อกับก่อนหน้านี้แล้ว คำนวนไปเลยทุก column
| hp | wt | am | mpg | PREDICTED MPG |
|---|---|---|---|---|
| 110 | 2.62 | 1 | 21 | 24.42205781 |
| 110 | 2.875 | 1 | 21 | 23.68802108 |
| 93 | 2.32 | 1 | 22.8 | 25.92276878 |
| 110 | 3.215 | 0 | 21.4 | 20.62559531 |
| 175 | 3.44 | 0 | 18.7 | 17.54179866 |
| … | … | … | … | … |
สังเกตว่า ค่า predicted ที่ได้ จะใกล้เคียงกับค่า mpg แต่ไม่เท่า ซึ่งมีทั้ง มากไป และ น้อยไป
ให้ย้อนกลับไปที่ ค่า Regression Statistics ให้ดูที่ค่า Multiple R ซึ่งสังเกตว่าค่านี้มาได้อย่างไร ในเมื่อตัวแปรต้นมีตั้ง 3 ตัว ถ้าเปรียบกับ Simple Linear Regression มันคำนวนค่าความสัมพันธ์ กันระหว่างค่าตัวแปรต้นและตัวแปรตามแค่ 1 ตัวได้ แต่ทำความสัมพันธ์ทั้ง 3 ตัวไม่ได้
วิธีที่นักสถิติทำก็คือ ใช้เทคนิคเปลี่ยนค่าตัวแปรต้นทั้ง 3 ตัวเปลี่ยนมาเป็น y-pred เป็นค่าเพียงตัวเดียว แล้วนำค่ามาหาความสัมพันธ์ กับ y
y-pred correl y หรือ y' correl y
เราก็จะได้ Multiple R
| Multiple R | 0.91645529 |
|---|---|
| R Square | 0.83989031 |
| Adjusted R Square | 0.82273569 |
| Standard Error | 2.53751194 |
| Observations | 32 |
ลองใช้สูตร Correl คำนวนความสัมพันธ์ระหว่าง y-pred กับ y
=CORREL(D:D,E:E)
##
0.916455294
คราวนี้เรามาสร้าง Column ขึ้นมาอีก 1 Column มันคือ ค่า Error หรือ ค่า Residual ความเดียวกัน
หลังจากสร้าง column ขึ้นมาแล้ว ค่าใน column นี้คือให้นำ ค่า y - y’ หรือ y-pred เราก็จะได้แบบนี้
| hp | wt | am | mpg | PREDICTED MPG | Error / Residual |
|---|---|---|---|---|---|
| 110 | 2.62 | 1 | 21 | 24.42205781 | -3.422057814 |
| 110 | 2.875 | 1 | 21 | 23.68802108 | -2.688021084 |
| 93 | 2.32 | 1 | 22.8 | 25.92276878 | -3.12276878 |
| 110 | 3.215 | 0 | 21.4 | 20.62559531 | 0.774404687 |
| 175 | 3.44 | 0 | 18.7 | 17.54179866 | 1.158201342 |
| … | … | … | … | … | … |
ให้สร้าง column error ขึ้นมาทำไม
ก็เพราะว่า ผลการทำนายเราจะไม่ แม่นยำ 100% ค่าติดลบก็เพราะทำนายได้มากเกินไป ค่าเป็นบวกก็เพราะทำนายน้อยเกินไป
สังเกตว่า ค่า predicted ที่ได้ จะใกล้เคียงกับค่า mpg แต่ไม่เท่า ซึ่งมีทั้ง มากไป และ น้อยไป อย่างที่กล่าวไปก่อนหน้านี้
ซึ่งเรากำลังจะประเมินว่า Model ที่สร้างขึ้นมานี้มีค่า Error เท่าไร โดยนำค่าที่ diff กันมาทำเป็นผลรวม แต่ว่า มันมีทั้งค่าบวก และ ค่าลบ ทำให้เมื่อทำผลรวมกันทั้งหมดแล้ว มันจะได้ 0 หรือค่าที่น้อยมากๆ
นักสถิติ จึงได้ใช้วิธีทำเป็นค่า ยกกำลัง 2 เพื่อกำจัดค่าติดลบออกไป
| hp | wt | am | mpg | PREDICTED MPG | Error / Residual | error ^2 |
|---|---|---|---|---|---|---|
| 110 | 2.62 | 1 | 21 | 24.42205781 | -3.42 | 11.71 |
| 110 | 2.875 | 1 | 21 | 23.68802108 | -2.69 | 7.23 |
| 93 | 2.32 | 1 | 22.8 | 25.92276878 | -3.12 | 9.75 |
| 110 | 3.215 | 0 | 21.4 | 20.62559531 | 0.77 | 0.60 |
| 175 | 3.44 | 0 | 18.7 | 17.54179866 | 1.16 | 1.34 |
แล้วนำค่า error ยกกำลังสอง มาทำเป็นผลรวมทั้งหมด ซึ่ง ก็คือค่า sum square error หรือ SSE
SSE = 180.29
ค่า SSE จะเป็นค่าที่บอก Error ของสมการเส้นตรงที่ดีที่สุด ซึ่งก็จะได้ค่าที่ต่ำที่สุดแล้ว
ซึ่งเราสามารถพิสูจน์ได้ โดยไปแก้ไขค่าตัวแปรต้น ให้เปลี่ยนแปลงไป ค่า SSE ก็จะเปลี่ยนแปลงตามไปด้วย
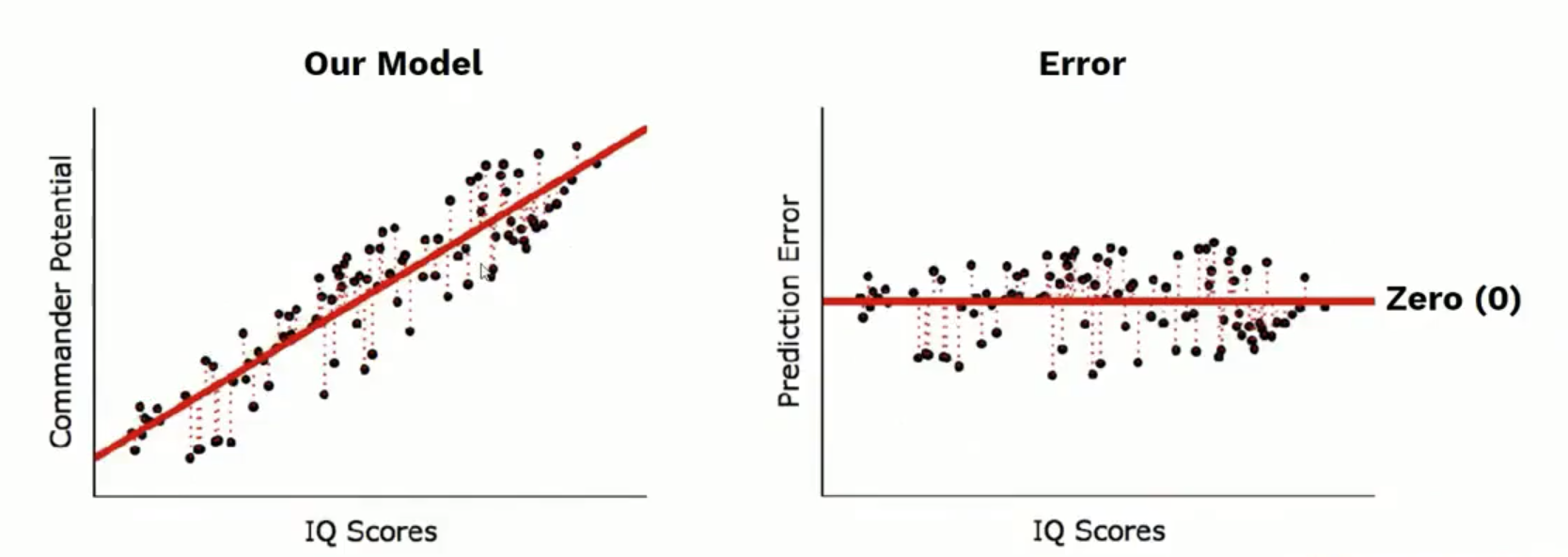

ซึ่งที่ผ่านมาเราได้ ค่า sum square error แล้วนำมาหาค่าเฉลี่ยของจำนวนรถทั้งหมด คือ 32 คัน แล้วนำมาถอด root เราก็จะได้ RMSE ของเส้นสมการที่ดีที่สุดแล้ว
SSE = 180.29
MSE = SSE/Obseave = 5.63
RMSE = 2.373625074
สรุปว่าค่า RMSE ยิ่งต่ำ Model เราหรือสมการยิ่งดี

คราวนี้มาลองทำ Linear Regression ด้วยภาษา R กัน
มาลองดู Correlation กันก่อน โดยใช้ dataset เดิม mtcars
ใช้คำสั่งเพื่อดูข้อมูลเบื้องต้น
head(mtcars)
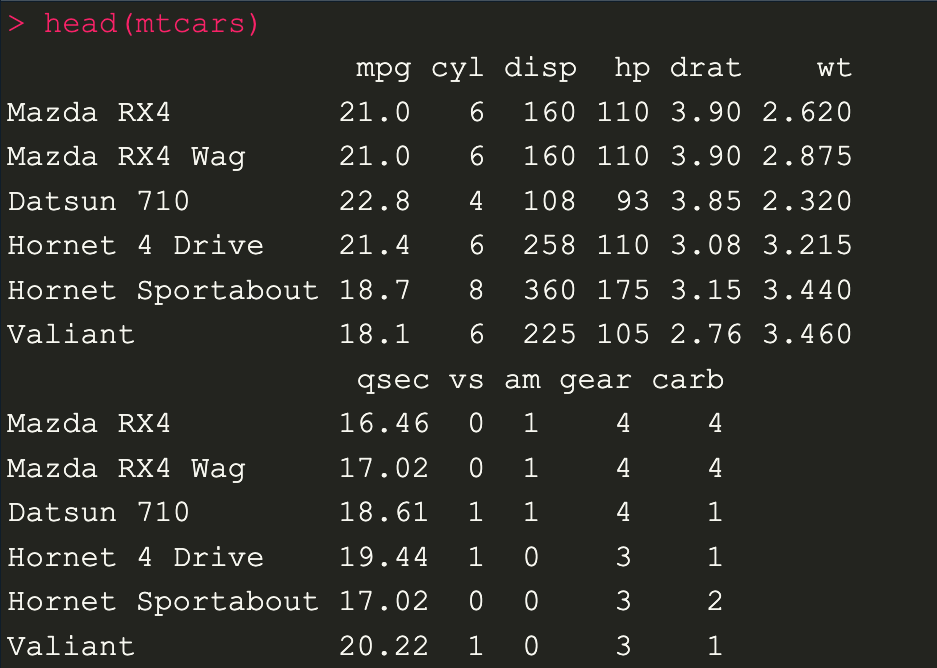
เราก็จะเห็น Column ของ dataset ซึ่งเราก็จะเอาชื่อของ Column มาทำ Correlation
cor(mtcars$hp, mtcars$mpg)
##
[1] -0.7761684
เมื่อเปรียบเทียบกับค่าที่ใช้สูตรใน excel ในส่วนของ simple linear regression ก็จะเห็นว่ามีค่าเท่ากัน หรือ อยากจะหาความสัมพันธ์กับคู่อื่นก็ได้ อย่างเช่น
cor(mtcars$wt, mtcars$mpg)
##
[1] -0.8676594
คราวนี้เราจะนำค่าที่ได้ลอง plot graph ด้วย scatter plot ดูด้วยคำสั่ง plot(X, Y) แกน X จะใส่เป็นตัวแปรที่ 1 และ Y ใส่เป็นตัวแปรที่ 2
plot(mtcars$hp, mtcars$mpg)
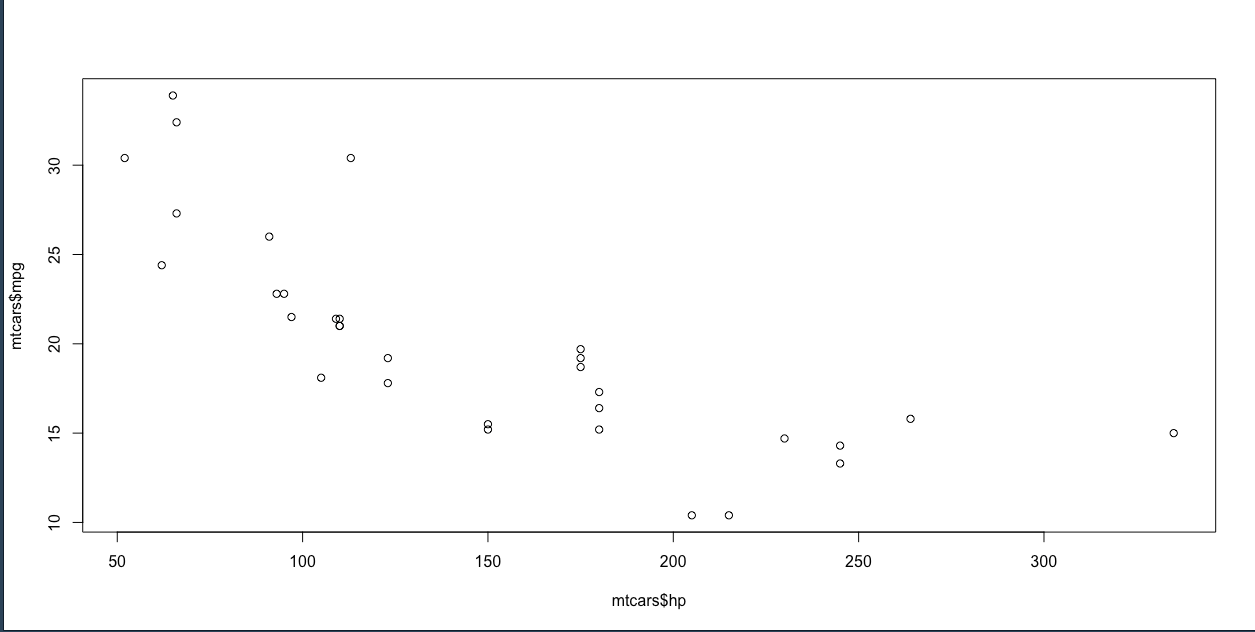
สังเกตว่า Correlation เป็น ลบ กราฟที่ได้จะแทยงลงตามภาพ
plot(mtcars$wt, mtcars$mpg)
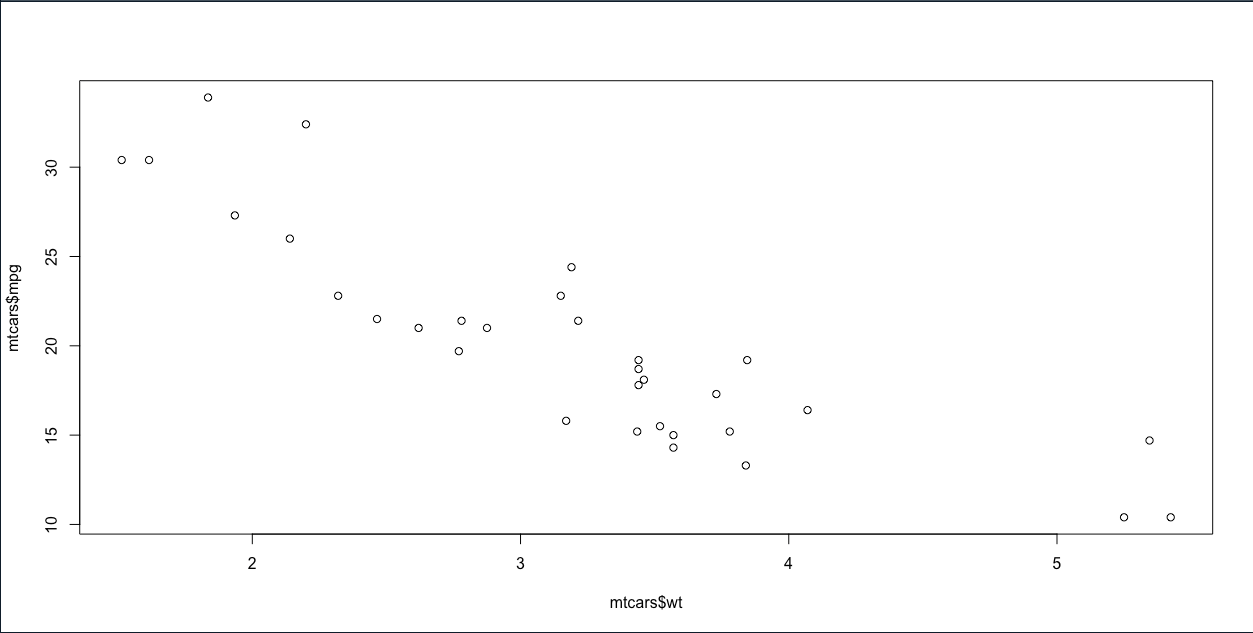
plot(mtcars$wt, mtcars$hp)
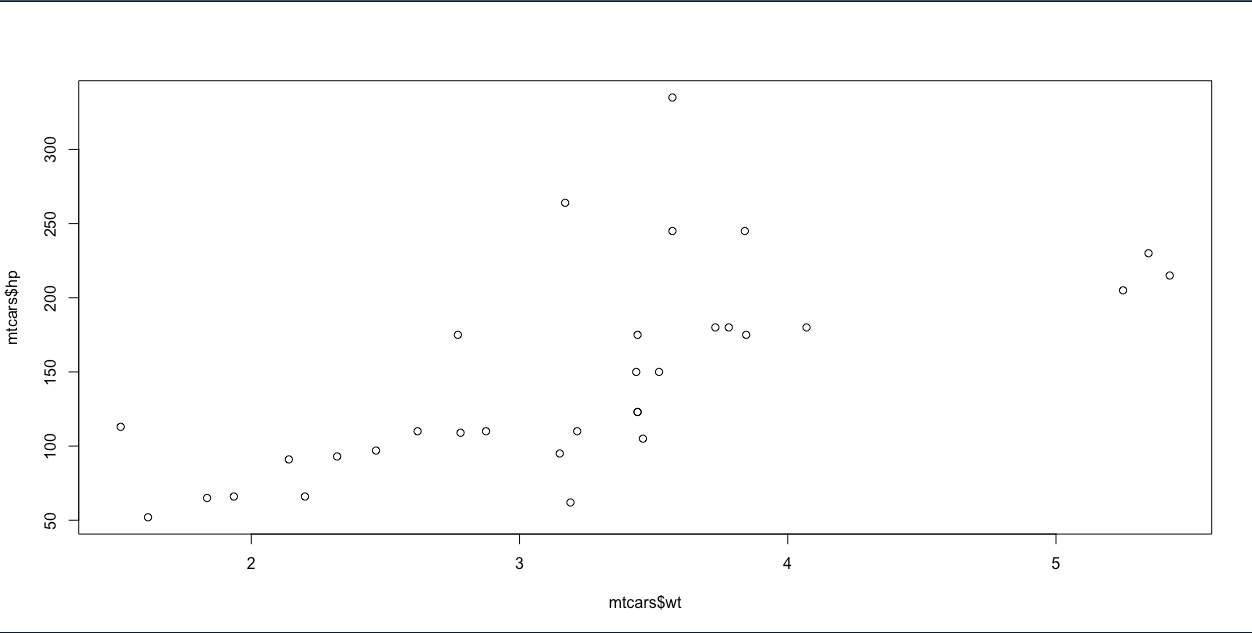
ลองข้อมูลที่อยู่ dataframe ที่ดึงออกมา 3 column mpg, wt, hp
mtcars[ , c("mpg", "wt", "hp")]
##
mpg wt hp
Mazda RX4 21.0 2.620 110
Mazda RX4 Wag 21.0 2.875 110
Datsun 710 22.8 2.320 93
Hornet 4 Drive 21.4 3.215 110
Hornet Sportabout 18.7 3.440 175
... 5 ROW ...
ที่ผ่านมาเราทำ Correlation แบบตัวแปรเดียว คราวนี้เราจะลองทำ Correlation Metrix โดยใช้ 3 ตัวแปรโดยใช้คำสั่ง cor เพื่อสร้าง ตารางความสัมพันธ์ของทั้ง 3 ตัวแปร จะได้แบบนี้
cor(mtcars[ , c("mpg", "wt", "hp")])
##
mpg wt hp
mpg 1.0000000 -0.8676594 -0.7761684
wt -0.8676594 1.0000000 0.6587479
hp -0.7761684 0.6587479 1.0000000
เราสามารถใช้ library ของ dplyr ได้เช่นเดียวกัน
## dplyr (tidyverse)
library(dplyr)
mtcar %>%
select(mpg, wt, hp) %>%
cor()
mpg wt hp
mpg 1.0000000 -0.8676594 -0.7761684
wt -0.8676594 1.0000000 0.6587479
hp -0.7761684 0.6587479 1.0000000
เราสามารถทดสอบ นัยสำคัญได้ เราทดสอบดูว่า ความพันธ์ไม่ได้เกิดมาแบบบังเอิญขึ้น เกิดขึ้นจริงๆ
ตอนที่เราหาค่าความสัมพันธ์ระหว่าง hp และ mpg โดยใช้ cor() ฟังก์ชัน เราแค่เพิ่ม .test เข้าไปที่ cor ฟังก์ชัน
## compute correlation (r) and sig test
cor(mtcars$hp, mtcars$mpg)
##
[1] -0.7761684
cor.test(mtcars$wt, mtcars$hp)
###
Pearson's product-moment correlation
data: mtcars$wt and mtcars$hp
t = -6.7424, df = 30, p-value = 1.788e-07
alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval:
-0.8852686 -0.5860994
sample estimates:
cor -0.7761684
จากข้อมูลค่า p-value ที่ได้ออกมา ต่ำกว่า 5% หรือ 0.05 แสดงว่า ค่า cor -0.7761684 มีนัยสำคัญทางสถิติ
โดยมีค่าความเชื่อมั่นที่ 95% -0.8852686 ถึง -0.5860994 แม้ว่าจะสุ่มตัวอย่างใหม่มาทั้งหมด 95 ใน 100 ครั้ง
มาทำ Linear Regression ด้วย R
ในภาษา R เราใช้ lm()
## Linear Regression
## mpg = f(hp)
lm(mpg ~ hp, data = mtcars)
Call:lm(formula = mpg ~ hp, data = mtcars)
Coefficients:
(Intercept) hp
30.09886 -0.06823
สามารถอ่านได้ว่า linear regression ที่ mpg เป็นฟังก์ชันของ hp (คำว่าเป็นฟังก์ชัน ใช้ตัวหนอน ~) โดยที่ dataคือ mtcars dataset ซึ่งเป็นการ Train Model หรือสร้าง สมการ mpg = f(hp) ขึ้นมา
lmFit <- lm(mpg ~ hp, data = mtcars)
ซึ่งลองเไปเทียบกับค่าใน excel ดูได้ว่ามีค่าเท่ากัน
ให้เราเก็บค่าเอาไว้ในตัวแปร แล้วนำตัวแปรมาสรุปออกมา เราจะได้ descriptive summery พวก Anova หรือ ค่าสัมประสิทธิ์
summary(lmFit)
###
Call:
lm(formula = mpg ~ hp, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-5.7121 -2.1122 -0.8854 1.5819 8.2360
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.09886 1.63392 18.421 < 2e-16 ***
hp -0.06823 0.01012 -6.742 1.79e-07 ***
---
Signif. codes:
0 ‘******’ 0.001 ‘****’ 0.01 ‘**’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.863 on 30 degrees of freedom
Multiple R-squared: 0.6024, Adjusted R-squared: 0.5892
F-statistic: 45.46 on 1 and 30 DF, p-value: 1.788e-07
เรามาลองดูข้อมูล Model lmFit ที่จะเราสร้างขึ้นใน R มันจะเก็บเป็น Object ซึ่ง เราสามารถที่ดึงออกมาดูได้ อย่างเช่น เราจะดึงค่าสัมประสิทธิ์ของ model simple linear regression
lmFit$coefficients
##
(Intercept) hp
30.09886054 -0.06822828
lmFit$coefficients[1]
##
(Intercept) 30.09886
lmFit$coefficients[2]
##
hp -0.06822828
ซึ่งจริงๆแล้วข้าง lmFit มีตัวแปรอื่นๆให้ดึงออกมาได้อีก
ทำการ prediction ค่า hp แล้วจะได้ค่า mpg เป็นเท่าไร ใน R สามารถเขียนได้แบบนี้
สมมติว่าค่า hp คือ 200
lmFit$coefficients[[1]] + lmFit$coefficients[[2]] * 200
##
[1] 16.4532
เราก็จะได้ค่า mpg เท่ากับ 16.45 ในการทำนายค่า รถเพียง 1 คัน แต่ถ้าเราอยากจะทำนายรถหลายคัน เราจะต้องทำ data frame ขึ้นมาก่อน สมมติว่าเราจะ ทำนายรถยนต์ 5 คัน
new_cars <- data.frame(
hp = c(250, 320, 400, 410, 450)
)
เราจะใช้ฟังก์ชัน predict() มาใช้ในการทำนาย
เป็นค่าที่ได้ทำนาย ของ mpg รถยนต์ทั้ง 5 คัน
predict(lmFit, newdata = new_cars)
###
1 2 3 4 5
13.0417910 8.2658116 2.8075493 2.1252665 -0.6038646
คราวนี้เราจะเอาข้อมูลที่ predict ออกมาใส่กลับเข้าไปใน dataframe โดยใช้ $ ต่อท้ายตัวแปรเพื่อสร้าง column
new_cars$hp_pred <- predict(lmFit, newdata = new_cars)
new_cars
###
hp hp_pred
1 250 13.0417910
2 320 8.2658116
3 400 2.8075493
4 410 2.1252665
5 450 -0.6038646
จริงๆแล้วจะต้องตั้งชื่อว่า mpg_pred
เราสามารถลบ column ได้ด้วยการเปิด ชื่อ Column แล้วใส่ Null เข้าไป
new_cars$hp_pred <- NULL
แล้วตั้งชื่อใหม่
new_cars$mpg_pred <- predict(lmFit, newdata = new_cars)
new_cars
คราวนี้เรามาสังเกตค่า hp ที่ 450 จะเห็นว่า mpg เป็นค่าติดลบ ซึ่งในความเป็นจริงมันเป็นไปไม่ได้
แต่ว่าถ้าย้อนกลับไปดูที่ original dataset ค่าต่ำสุดคือ 54, ค่าสูงสุดคือ 324 ซึ่ง ในตัวอย่างนี้ เป็นค่าที่เกินไปจากค่าใน dataset หรือ ค่าที่ model ไม่เคยเห็นมาก่อน
hp mpg_pred
1 250 13.0417910
2 320 8.2658116
3 400 2.8075493
4 410 2.1252665
5 450 -0.6038646
ให้ลองนึกว่า Model Linear Regression มันเป็นเส้นตรง ซึ่งมันมีการเรียนรู้มา แค่เท่าที่เคยเห็นข้อมูล คือค่าสูงสุดและค่าต่ำสุด เป็นข้อจำกัด ของ linear regression ซึ่ง เวลาที่มีค่าเปลี่ยนแปลง ค่ามันก็จะเปลี่ยนแปลงไปแบบ Linear ไปด้วย ซึ่งวิธีแก้จะต้องเก็บข้อมูลที่มากขึ้น
เราสามารถสรุปค่าใน Column hp ได้
> summary(mtcars$hp)
Min. 1st Qu. Median Mean 3rd Qu. Max.
52.0 96.5 123.0 146.7 180.0 335.0
คราวนี้เรามาหาค่า Root Mean Square กันบ้าง
ก่อนที่เราจะไปหา rmse ได้เราจะต้องรู้ค่า Error ของ Model สมการก่อน ซึ่งก็เป็นสมการ Multiple Linear Regression โดยที่สมการหน้าตาจะเป็นแบบนี้
## Root Mean Squared Error (rmse)
## multiple Linear Regression
## mpg = f(hp, wt, am)
## mpg = intercept + b0**hp + b1**wt + b2*am
เราสามารถเขียน ฟังก์ชันด้วย R เหมือนกับ Simple Linear Regression ได้เลยที่
lmFit2 <- lm(mpg ~ hp + wt + am, data = mtcars)
และเราสามารถที่จะดึงค่าสัมประสิทธิ์ของแต่ละตัวได้เลยจากฟังก์ชัน coef ซึ่งปกติมันจะอยู่ในตัวแปร object
และลองทดสอบค่าเดียวกันกับใน excel
coefs <- coef(lmFit2)
coefs[[1]] + coefs[[2]]*200 + coefs[[3]]*3.5 + coefs[[4]]*1
##
[1] 18.51583
เราสามารถที่สร้าง model ขึ้นมาจาก ตัวแปรทุกตัวที่อยู่ใน dataframe mtcars ได้เลยไม่ต้องเลือก column เป็นใช้ฟังก์ชัน . ซึ่งเป็นตัวบอกว่าเอาทุกตัวแปรมาเป็น input function
lmFit_Full <- lm(mpg ~ . , data = mtcars)
lmFit_Full
Call:
lm(formula = mpg ~ ., data = mtcars)
Coefficients:
(Intercept) cyl disp
12.30337 -0.11144 0.01334
hp drat wt
-0.02148 0.78711 -3.71530
qsec vs am
0.82104 0.31776 2.52023
gear carb
0.65541 -0.19942
เราก็จะได้ค่าสัมประสิทธิ์ ของ Model สมการ Multiple Linear Regression
แต่ถ้าหากว่า เราไม่ได้ต้องการค่าสัมประสิทธิ์สักตัวหนึ่งที่อยู่ในนี้ เราสามารถที่จะ ใช้เครื่องหมาย ลบ (-) เพื่อไม่ต้องมาคำนวนได้ ซึ่งค่าสัมประสิทธิ์จะเปลี่ยนแปลงไป เมื่อตัวแปรต้น หายไปหนึ่งตัว
lmFit_Full <- lm(mpg ~ . - gear, data = mtcars)
lmFit_Full
Call:
lm(formula = mpg ~ . - gear, data = mtcars)
Coefficients:
(Intercept) cyl disp
15.64181 -0.27315 0.01395
hp drat wt
-0.02063 0.84089 -3.86609
qsec vs am
0.79507 0.35800 2.80345
carb
-0.04506
แต่ในตัวอย่างนี้เราจะใช้แบบ full model ในการ predict เพื่อหาค่า rmse
คราวนี้เราจะเอา model ที่ Train ออกมาแล้ว จาก สมการ Linear Regression มาการทำนายด้วยฟังก์ชัน predict แล้วใส่กลับเข้าไปใน object mtcars เพื่อดูค่าแบบภาพรวม
mtcars$predicted <- predict(lmFit_Full)
mtcars$predicted เป็นการสร้าง column ใหม่ชื่อ predicted ขึ้นมา
ลองใช้ฟังก์ชัน head(mtcars)
head(mtcars)
###
mpg cyl disp hp drat
Mazda RX4 21.0 6 160 110 3.90
Mazda RX4 Wag 21.0 6 160 110 3.90
Datsun 710 22.8 4 108 93 3.85
Hornet 4 Drive 21.4 6 258 110 3.08
Hornet Sportabout 18.7 8 360 175 3.15
Valiant 18.1 6 225 105 2.76
wt qsec vs am gear
Mazda RX4 2.620 16.46 0 1 4
Mazda RX4 Wag 2.875 17.02 0 1 4
Datsun 710 2.320 18.61 1 1 4
Hornet 4 Drive 3.215 19.44 1 0 3
Hornet Sportabout 3.440 17.02 0 0 3
Valiant 3.460 20.22 1 0 3
carb predicted
Mazda RX4 4 22.59951
Mazda RX4 Wag 4 22.11189
Datsun 710 1 26.25064
Hornet 4 Drive 1 21.23740
Hornet Sportabout 2 17.69343
Valiant 1 20.38304
จากตารางค่า mpg เป็นค่าจริง และ predicted เป็นค่าที่ทำนาย
เราจะหาค่า error ซึ่งก็เอาทั้ง 2 ค่านี้มาลบกัน แล้วหาค่า root mean square
^2 หรือ ** 2 เป็นการยกกำลังเหมือนกัน
## Train RMSE
square_error <- mtcars$mpg - mtcars$predicted
square_error <- (mtcars$mpg - mtcars$predicted) ** 2
rmse <- mean(square_error)
rmse <- sqrt(mean(square_error))
(rmse <- sqrt(mean(square_error)))
###
[1] 2.146905
ค่า rmse จะเท่ากับ 2.146905 หรือแปลได้ว่า model ของเราทำนาย mpg ผิดไปประมาณ 2.14 โดยเฉลี่ยตลอดทั้งเส้น ซึ่งเป็นค่า Error ของ dataset ที่ Train model ขึ้นมา
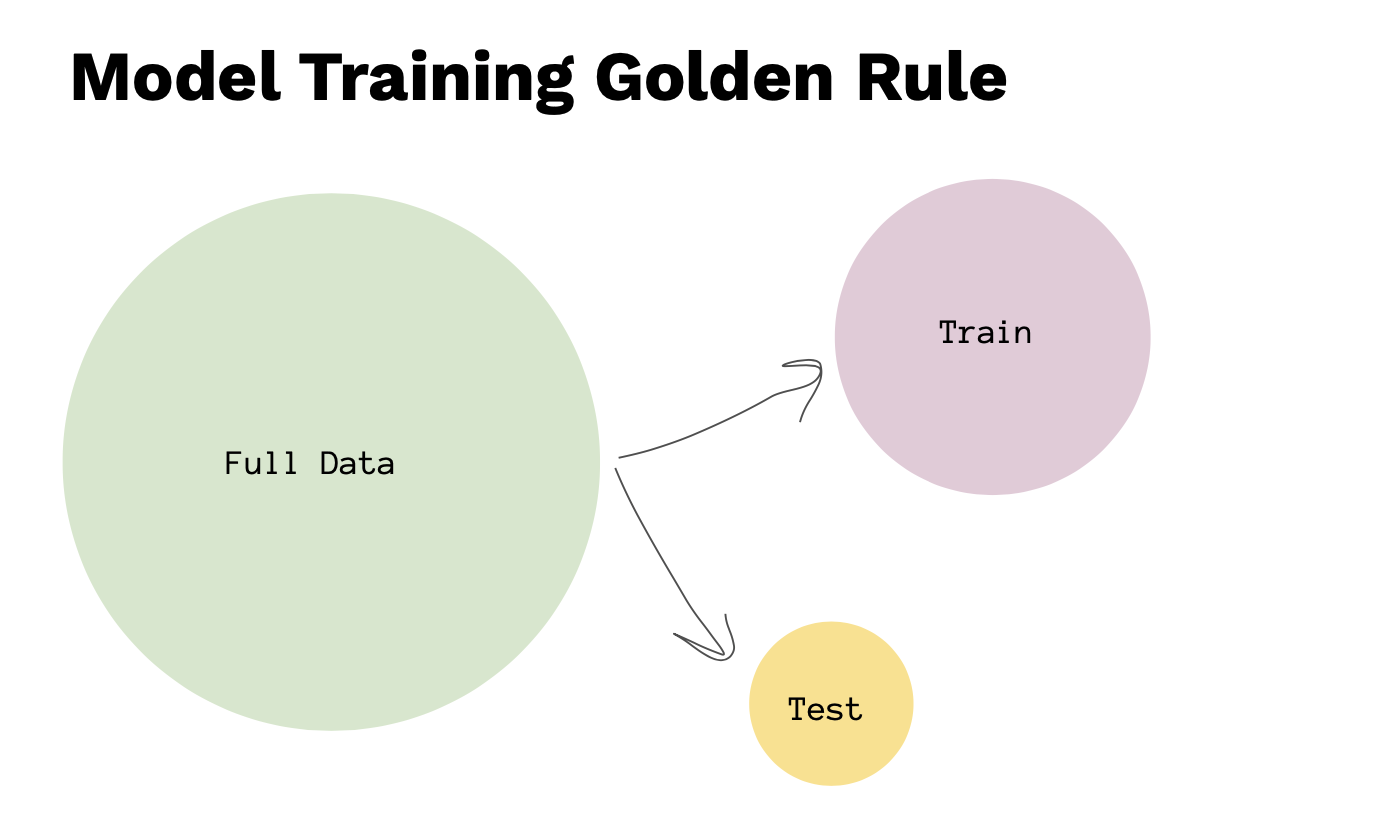
ซึ่งการ Build model เบื้องต้น การ Evaluation Model
โดยที่ Full Dataset มีข้อมูลทั้งหมด 1000 แถว ในการจะ Train Model เราจะต้องมีการ split data ก่อน แล้วเราแบ่งข้อมูลออกเป็น 2 ส่วน คือ Train Dataset และ Test Dataset ไม่ต้องเท่ากัน อย่างเช่น 70% และ 30% หรือ 80% และ 20% ซึ่งทั้ง 2 ส่วนจะต้องรวมกัน 100%
ซึ่งเราจะไม่สามารถวัดผลได้เลย ถ้าหากว่าเราไม่มีการแบ่ง Data ออกเป็น 2 ส่วนซึ่ง จะต้องแบ่งในส่วน Train Dataset นำไป Train Model ขึ้นมาแล้ว นำ Test Dataset มาทดสอบ หรือเรียกว่า Unseen Dataset ก็ได้ หรือ เราจะสร้าง dataset ขึ้นมาใหม่แต่ว่า มันจะเป็นค่าที่อาจจะไม่ได้อยู่ในกลุ่มเดียวกัน เวลาที่เราจะต้องวัดผล model เราจะต้องนำ Test Dataset มาทดสอบ
การ Split Data
เรามาทำการ Split Data อย่างง่ายๆกันก่อน โดยการ Randomly Split
สามารถใช้ฟังก์ชัน sample() ใน R
ค่า 1:10 หมายถึงค่าที่จะ ramdom ออกมา 1 ถึง 10 และ เลข 3 หมายถึงให้ random ออกมา 3 ตัว
## Split Data
sample(1:10, 3)
## run 3 time
[1] 9 8 7
[1] 1 3 9
[1] 3 7 2
ค่าที่ทำการ sample มันจะถูกสุ่มไปเรื่อยๆ
ซึ่งหากอยากจะ lock ผลเอาไว้ที่ค่าที่สุ่มในครั้งแรก ให้ใช้คำสั่ง set.seed()
set.seed(42)
sample(1:10, 3)
## run 3 time
[1] 1 5 10
[1] 1 5 10
[1] 1 5 10
เราจะกำหนด sample size ก่อน ซึ่งเป็นการรับค่าจาก จำนวนแถวของ dataset มาเก็บเอาไว้ในตัวแปร n จากนั้นก็มาสร้าง sample size ด้วย ฟังก์ชัน sample โดยกำหนดขนาด id เอาไว้ที่ sample size ทั้งหมด คูณด้วย 80% ก็คือเอาจำนวน 80% จากรถทั้งหมด 32 คัน มาเป็น train data โดยข้างในจะเป็น ตัวเลขของตำแหน่งใน array
n <- nrow(mtcars)
id <- sample(1:n, size=n*0.8)
##
> id
[1] 25 10 4 18 26 17 15 24 7 30 5 14
[13] 20 29 28 3 9 16 11 23 22 12 13 2
[25] 31
หลังจากที่ได้ id มาแล้วเราจะเอา id ตัวนี้มาเป็น train_data โดยเอา id ใส่เข้าไปเพื่อดึงข้อมูลจากตำแหน่งที่กำหนดเอาไว้ใน mtcars dataframe
train_data <- mtcars[id, ]
test_data <- mtcars[-id, ]
โดยเครื่องหมายลบ ที่เห็นกำหนดเอาไว้ใน ตำแหน่งใน mtcars หมายถึง ค่าตรงข้ามทั้งหมดที่ได้จาก id
## Split Data
set.seed(42)
sample(1:10, 3)
n <- nrow(mtcars)
id <- sample(1:n, size=n*0.8)
train_data <- mtcars[id, ]
test_data <- mtcars[-id, ]
ให้ run ค่าพร้อมกันโดยการ Hilight
คราวนี้เราได้ Data set ที่แบ่งออกมาเป็น Train และ Test แล้ว เราก็จะเอามาสร้าง model จากสมการ linear regression
ซึ่งสังเกตว่า เราจะไม่ใช้ mtcars แล้ว
- ซึ่งเป็น full dataframe เราเอา train_data ที่ split ไว้มาใส่แทน ในบรรทัดที่ 1
- จากนั้นก็เอา model1 ที่ได้มา ทำการ predict เอาก็จะได้ predict_train ในบรรทัดที่ 2
- แล้วก็เอาค่า actual ที่อยู่ใน train_data ที่อยู่ใน column mpg นำมาลบ กับค่าที่ predict_train เพื่อได้ค่า error ในบรรทัดที่ 3
- จากนั้นก็นำมาทำ rmse : root mean square ในบรรทัดที่ 4
## Train Model
1: model1 <- lm(mpg ~ hp + wt, data = train_data)
2: predict_train <- predict(model1)
3: error <- train_data$mpg - predict_train
4: (rmse <- sqrt(mean((error** 2))))
###
[1] 2.565222
หรือจะเขียนแบบสั้นในบรรทัดเดียวก็ได้
model1 <- lm(mpg ~ hp + wt, data = train_data)
predict_train <- predict(model1)
(rmse_train <- sqrt(mean( (train_data$mpg - predict_train ** 2))))
คราวนี้ ก็เอามาทดสอบ
โดยเราจะใช้ ฟังก์ชัน predict เหมือนเดิมแต่ เพิ่มอีก argument เข้าไปโดยใช้ newdata = test_data แล้วนำมาทดสอบกับค่า actual เหมือนเดิม
p_test <- predict(model1, newdata = test_data)
error_test <- test_data$mpg - p_test
(rmse_test <- sqrt(mean( error_test ** 2)))
##
[1] 2.234054
ลองเอาค่า predict ทั้ง train และ test มาเปรียบเทียบกัน
## result
cat("RMSE Train : ", rmse_train, "\\nRMSE Test : ", rmse_test)
##
RMSE Train : 2.565222
RMSE Test : 2.234054
Over fitting
จากตัวอย่างที่เห็นในด้านบน ให้เปรียบเทียบระหว่างค่า Error ของทั้ง RMSE Train และ RMSE Test จะเห็นว่า ค่าที่ Test มีค่า Error ที่ใกล้เคียงกัน และ ดีกว่าด้วย ซึ่งมีค่าน้อยกว่า แต่ถ้าสมมติว่า ค่า RMSE Test มีค่ามากกว่า อย่างเช่น ยกตัวอย่าง ลองปรับจูนค่า dataset ที่ทำการ train และ test ดู
ปรับ train data size เป็น 0.9 เราจะได้ RMSE Test ที่แย่ ก็คือมีค่า Error ที่สูงกว่าค่า Train ซึ่งเราจะต้องมาปรับจูนตัวแปรต้นต่างๆให้ดียิ่งขึ้น
RMSE Train : 2.236741
RMSE Test : 3.803203
ลักษณะนี้เรียกว่า Overfitting ซึ่งเราก็ต้องปรับจูนให้มีค่า Error น้อยลง
เราคาดหวังว่า ตัวเลขทั้ง 2 ตัวนี้จะต้องมีค่าใกล้เคียงกัน model นี้จึงจะเรียกว่ามีความ fit ที่ดี
Logistics Regression
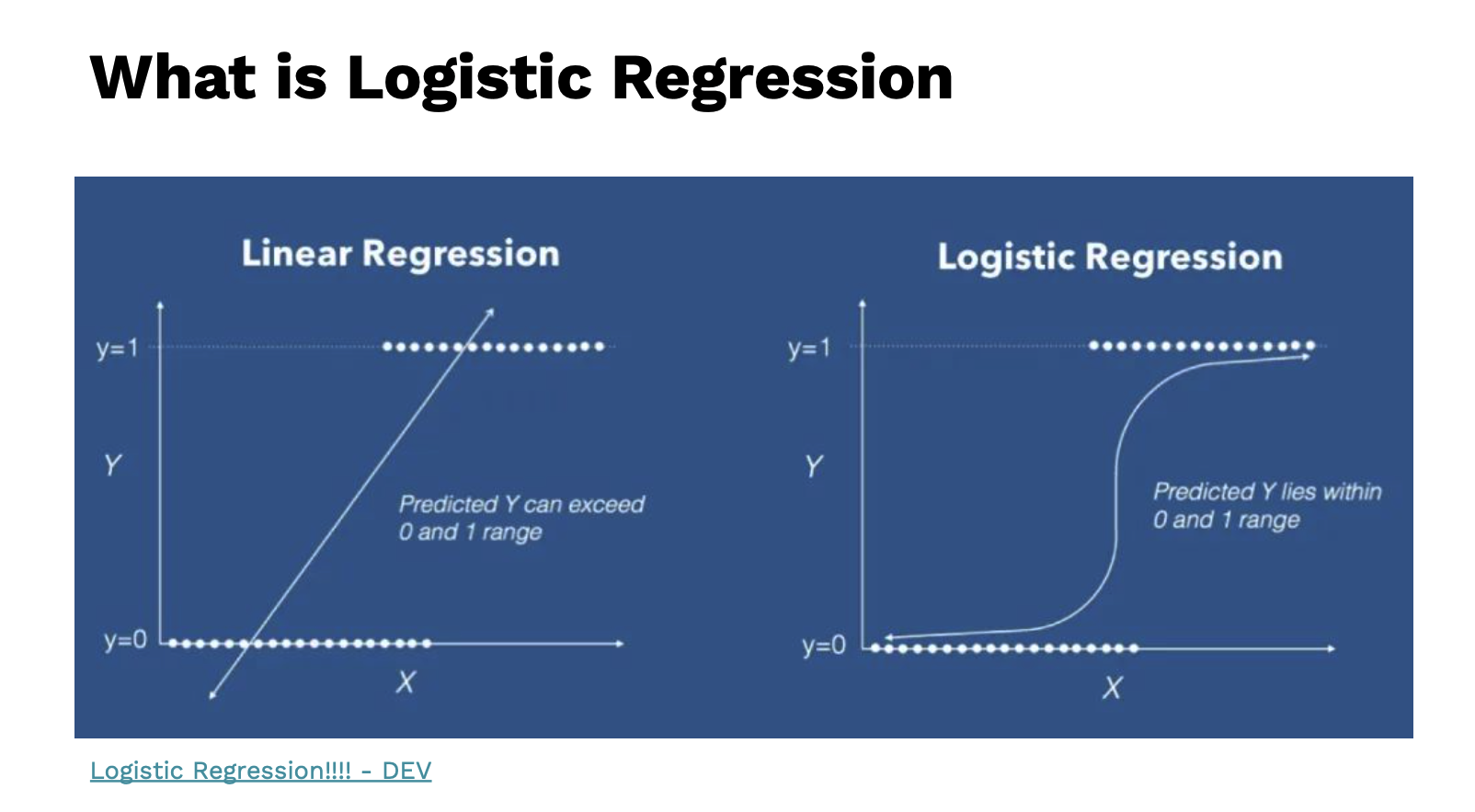
ถ้าเปรียบเทียบปัญหาของ Linear Regression เวลาที่มีค่าที่สูงขึ้นไปเรื่อยๆ การทำนายมันจะเริ่มไม่ค่อยดี มันควรจะมีค่าที่อยู่ในช่วงเดิม และ อีกปัญหาหนึ่ง ถ้านำ Linear Regression มาทำนายค่าที่เป็น แบบ Binary หรือมีค่าที่ 0 กับ 1 ซึ่งมันจะมีค่าที่เป็นเส้นตรงไปเรื่อยๆ เพราะ ค่าที่ได้มีโอกาสที่จะเป็นค่าติดลบ
ดังนั้น นักสถิติจึงมีสมการหนึ่งที่ สามารถเปลี่ยนค่าทั้งหมด หรือ เป็นการทำอัตราส่วนบีบค่าทั้งหมดให้อยู่ในช่วง 0 ถึง 1 ตามรูปด้านบนทางด้านขวา สมการนั้นเรียกว่า sigmoid function
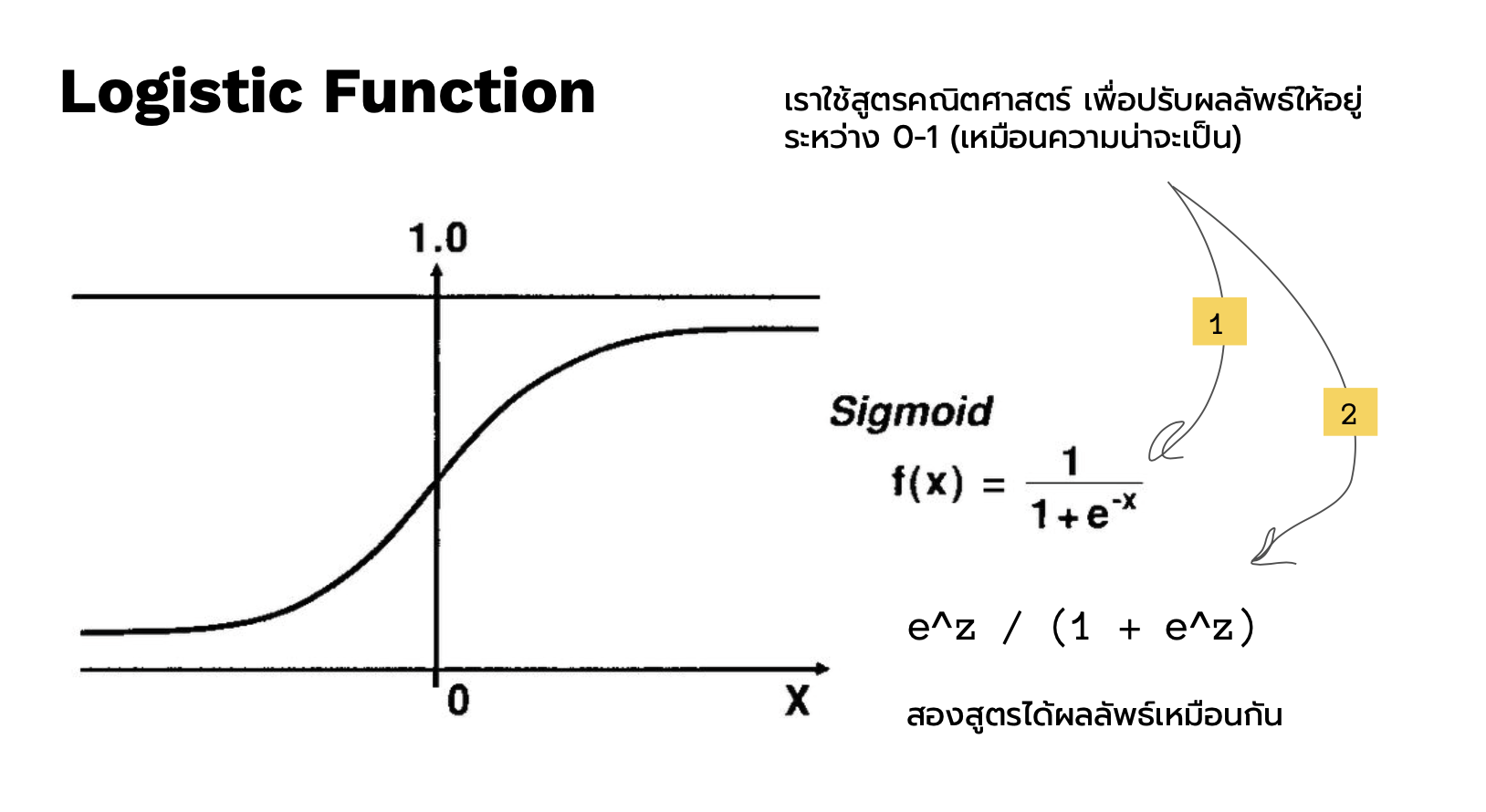
นี่คือ สมการ sigmoid function ที่ทำหน้าที่ บีบค่าให้อยู่ในช่วง 0 ถึง 1 และค่าที่ได้นี้เป็นค่าความน่าจะเป็น
ซึ่งโจทย์สำหรับตัวอย่างนี้จะเป็นการทำนายค่าที่เป็น 0 กับ 1 ก็คือ column am หมายถึง จะทำนายว่า ตัวแปรต้นที่ใส่เข้าไปเพื่อ train model จะสามารถทำนายว่า เป็นเกียร์ Auto หรือ เกียร์ Manual ได้กี่เปอร์เซ็น
## Logistic Regression
library(dplyr)
> mtcars %>% head()
am gear carb
Mazda RX4 1 4 4
Mazda RX4 Wag 1 4 4
Datsun 710 1 4 1
Hornet 4 Drive 0 3 1
Hornet Sportabout 0 3 2
Valiant 0 3 1
ก็จะเห็นว่า am จะมีค่า. 0 ก้บ 1
จะทำนายโดยค่า mpg จะมาดูว่า ค่า mile per gallon หรือการบริโภคน้ำมันมีผลต่อการใช้เกียร์หรือเปล่า
กลับมาที่ code ซึ่งจะต้องเปลี่ยนค่า 0 และ 1 ให้เป็นข้อความ คือ Auto และ Manual
mtcars$am <- factor(mtcars$am,
levels = c(0,1),
labels = c("Auto", "Manual"))
ฟังก์ชัน factor เป็นการเปลี่ยนค่า
เมื่อลองเช็ค class และ value
class(mtcars$am)
table(mtcars$am)
###
> class(mtcars$am)
[1] "factor"
> table(mtcars$am)
Auto Manual
19 13
จะเห็นว่ามี auto อยู่ 19 คัน และ Manual อยู่ 13 คัน ซึ่ง object นี้เป็น factor
เรานี้เรามา split data
## Split Data
set.seed(42)
sample(1:10, 3)
n <- nrow(mtcars)
id <- sample(1:n, size=n*0.7)
train_data <- mtcars[id, ]
test_data <- mtcars[-id, ]
คราวนี้ก็เอา data set ที่ split ไว้มา train model ด้วย logistic regression
## train model
logit_model <- glm(am ~ mpg, data = train_data, family = "binomial")
predict_train <- predict(logit_model)
ลองดูค่า ที่ทำการทำนายออกมา ด้วย predict_train
> predict_train
Pontiac Firebird Merc 280
-0.66307439 -0.66307439
Hornet 4 Drive Fiat 128
0.02877665 3.48803187
Fiat X1-9 Chrysler Imperial
1.88419536 -2.07822426
Cadillac Fleetwood Camaro Z28
-3.43047857 -2.51849310
Duster 360 Ferrari Dino
-2.20401536 -0.50583552
Hornet Sportabout Merc 450SLC
-0.82031327 -1.92098538
Toyota Corolla Ford Pantera L
3.95974849 -1.73229873
Lotus Europa Datsun 710
2.85907638 0.46904550
Merc 230 Lincoln Continental
0.46904550 -3.43047857
Merc 280C AMC Javelin
-1.10334324 -1.92098538
Dodge Challenger Merc 450SE
-1.82664206 -1.54361209
Merc 450SL Mazda RX4 Wag
-1.26058211 -0.09701445
Maserati Bora
-1.98388093
สังเกตเห็นว่า ในตอนแรกบอกไว้ว่า ค่าที่ได้มันจะต้องเป็น 0 กับ 1 แล้วทำไมค่าที่ได้ยังเป็นค่าติดลบ และไม่ใช่ 0 กับ 1 ซึ่งค่านี้ไม่ใช่ค่าที่เราใช้ แต่เรียกว่าค่า logit
ซึ่งการทำให้ค่าอยู่ระหว่าง 0 ถึง 1 ก่อน แปลงให้เป็นค่าความน่าจะเป็นก่อน ซึ่งในบรรทัดที่ function predict จะต้องเพิ่ม type เข้าไป
## train model
logit_model <- glm(am ~ mpg, data = train_data, family = "binomial")
predict_train <- predict(logit_model, type="response") ## probability
แล้วลองดูค่าอีกครั้ง
> predict_train
Pontiac Firebird Merc 280
0.34004933 0.34004933
Hornet 4 Drive Fiat 128
0.50719367 0.97034531
Fiat X1-9 Chrysler Imperial
0.86809227 0.11123139
Cadillac Fleetwood Camaro Z28
0.03135639 0.07457187
Duster 360 Ferrari Dino
0.09939049 0.37617028
Hornet Sportabout Merc 450SLC
0.30569717 0.12775172
Toyota Corolla Ford Pantera L
0.98128887 0.15029378
Lotus Europa Datsun 710
0.94578596 0.61515781
Merc 230 Lincoln Continental
0.61515781 0.03135639
Merc 280C AMC Javelin
0.24911400 0.12775172
Dodge Challenger Merc 450SE
0.13863879 0.17601080
Merc 450SL Mazda RX4 Wag
0.22087370 0.47576539
Maserati Bora
0.12090574
สังเกตว่าค่าที่ได้ จะอยู่ระหว่าง 0 ถึง 1 แล้ว
แต่ค่าที่ได้นี้เป็นค่าความน่าจะเป็น เราจะต้องกำหนดค่าที่เรียกว่า ค่า theashold เป็นค่าจูนนิ่งตามความเหมาะสมที่เราต้องการ แต่ค่า default ปกติจะอยู่ที่ 0.5
train_data$pred <- if_else(predict_train >= 0.5, "Manual", "Auto")
##
> train_data$pred
[1] "Auto" "Auto" "Manual" "Manual"
[5] "Manual" "Auto" "Auto" "Auto"
[9] "Auto" "Auto" "Auto" "Auto"
[13] "Manual" "Auto" "Manual" "Manual"
[17] "Manual" "Auto" "Auto" "Auto"
[21] "Auto" "Auto" "Auto" "Auto"
[25] "Auto"
ค่าในแต่ละแถวที่ออกมาตามเงื่อนไขของ ค่า Threshold
คราวนี้เรามาประเมินความแม่นยำดู
เรารู้ว่าค่า actual เป็นค่า 0 กับ 1 และค่าที่ทำนายหลังผ่านค่า threshold ออกมาแล้ว ก็เป็น 0 กับ 1 เช่นกันให้เอามาเทียบค่ากันเลย
train_data$am == train_data$pred
##
> train_data$am == train_data$pred
[1] TRUE TRUE FALSE TRUE TRUE TRUE
[7] TRUE TRUE TRUE FALSE TRUE TRUE
[13] TRUE FALSE TRUE TRUE FALSE TRUE
[19] TRUE TRUE TRUE TRUE TRUE FALSE
[25] FALSE
ถ้าทำนายถูกก็จะแสดงค่า TRUE หรือ ผิดก็ FALSE แล้วเราก็หาค่าเฉลี่ย ว่าได้เท่าไรแล้วก็ทำเป็นเปอร์เซ็น
> mean(train_data$am == train_data$pred)
##
[1] 0.76 หรือ 76%
คราวนี้เรามาทดสอบ.model นี้กับ. test data set ว่ามีประสิทธิภาพแค่ไหนในการทำนาย เกียร์รถยนต์
ซึ่งในการ ทดสอบ จะต้องห้ามลืมใส่ newdata เสมอเพื่อเป็นการบอกให้ฟังก์ชันรู้ว่า เป็นข้อมูล unseen
predict_test <- predict(logit_model, newdata = test_data, type="response") ## probability
test_data$pred <- if_else(predict_test >= 0.5, "Manual", "Auto")
mean(test_data$am == test_data$pred)
###
> mean(test_data$am == test_data$pred)
[1] 0.5714286 หรือ 57.14%
จะเห็นว่า ทายผิดเยอะมาก ซึ่งเกิดปัญหา Overfitting เพราะข้อมูลน้อยเกินไป ทำให้ overfit กับ ข้อมูล train มากเกินไป โดยปกติแล้ว Logistic Regression เป็น model ไม่ค่อย overfit เท่าไรถ้ามีข้อมูลที่มากเพียงพอ
คอร์สนี้ดีมากกกก (ไก่ ล้านตัว) ใครอ่านจบ แนะนำว่าให้ไปสมัครเรียน ติดตามได้ที่ link ด้านล่างนี้เลย จริงๆ
Course Online DATA ROCKIE Bootcamp


